Crittografia Moderna
- Crittografia simmetrica
- Crittografia asimmetrica
- Funzioni crittografiche di Hash
- Firma digitale
- Riferimenti esterni
La crittografia moderna si differenzia notevolmente dalla crittografia di cui si è parlato fin ora; l’avvento dei computer infatti ha rivoluzionato profondamente sia i sistemi crittografici sia il modo di vedere e utilizzare la crittografia.
Molti sistemi crittografici analizzati in precedenza e considerati ragionevolmente sicuri fino al XIX sec, possono oggi essere forzati in tempi brevissimi grazie alla velocità di elaborazione del computer. Inoltre possono essere ora utilizzati sistemi crittografici molto complessi e che, un tempo, avrebbero richiesto tempi di cifratura “a mano” troppo lunghi.
Nell’era dei computer la crittografia è “uscita dai campi di battaglia” e viene utilizzata da ogni persona, più o meno consapevolmente, nella vita di tutti i giorni: per prelevare soldi con un bancomat, nell’effettuare acquisti su internet o, semplicemente, chiamando con un telefono cellulare. La crittografia è quindi diventata uno strumento di massa, atto a proteggere i segreti di stato tanto quanto i dati che noi vogliamo, o almeno vorremmo, rimanessero privati.
Si può iniziare a parlare di crittografia moderna a partire dagli anni 1970 quando oltre ad esser stata trovata una soluzione al problema dello scambio della chiave (Diffie-Hellman) furono inventati i primi sistemi crittografici moderni simmetrci (DES) e asimmetrici (RSA) adatti ai calcolatori elettronici che proprio in quel periodo iniziavano a diffondersi.
Sebbene non consistano in veri e propri sistemi di crittografia, le funzioni crittografiche di hash hanno un ruolo piuttosto importante nell’ambito della crittografia moderna, essendo utilizzate in diversi ambiti come la verifica dell’integrità dei dati, la memorizzazione delle password e la firma digitale.
Crittografia simmetrica
Con crittografia simmetrica, o crittografia a chiave privata o precondivisa, si intende una tecnica di cifratura in cui si usa la stessa chiave sia per la cifratura che per la decifratura, rendendo l’algoritmo molto performante e semplice da implementare. Tuttavia presuppone che le due parti siano già in possesso delle chiavi, richiesta che non rende possibile uno scambio di chiavi con questo genere di algoritmi. Lo scambio avviene attraverso algoritmi a chiave asimmetrica o pubblica, generalmente più complessi sia da implementare che da eseguire ma che permettono questo scambio in modo sicuro. Dopodiché la comunicazione verrà crittata usando solo algoritmi a chiave simmetrica per garantire una comunicazione sicura ma veloce.
I crittosistemi moderni utilizzano diverse tecniche, anche molto complicate, per rendere pratica e sicura la cifratura. Studiando la storia della crittografia si può notare come nel tempo siano stati teorizzati e formalizzati matematicamente molti metodi.
Funzionamento
In questo genere di algoritmi si suppone che entrambe le parti conoscano già la chiave con cui cifrare e decifrare il messaggio. Il mittente ha un messaggio P (PlainText o testo in chiaro). Il mittente critta il messaggio P con la chiave k usando un algoritmo di crittografia simmetrica chiamato S. Il messaggio risultante sarà C (CypherText o messaggio cifrato). In formule diventa:
S(P, k) = C
A questo punto al destinatario arriva un messaggio cifrato che riesce a decrittare poiché è in possesso della chiave privata. Ora il ricevente applica l’algoritmo di decrittazione D con la stessa chiave che ha usato il mittente per crittare il testo. Diventa:
D(C, k) = P
Se un attaccante ha intercettato il messaggio lungo il mezzo di comunicazione, avrà il messaggio crittato ma non la chiave che è stata scambiata in modo sicuro dai due interlocutori. Se l’attaccante vorrà leggere il messaggio crittato potrà solo usare metodi di decrittazione che richiedono elevate capacità di calcolo.
Il problema dello scambio della chiave deve essere risolto usando sistemi differenti come l’utilizzo della crittografia asimmetrica.
Dagli anni ‘70, che segnano l’inizio della crittografia contemporanea, è stato realizzato un grandissimo numero di crittosistemi. Di seguito sono descritti i sistemi più utilizzati che hanno costituito uno standard per la cifratura simmetrica negli ultimi 50 anni.
Cifrari a Blocchi
I cifrari a blocchi rappresentano la famiglia più numerosa e importante dei crittosistemi contemporanei. Tutti i sistemi di cifratura visti finora erano pensati per cifrare testi applicando l’algoritmo di cifratura carattere per carattere. La cifratura a blocchi invece prevede la suddivisione dei dati da cifrare in blocchi solitamente rappresentati con una codifica binaria (ad esempio ASCII o unicode se si tratta di un testo) per poterli gestire con i calcolatori elettronici. La cifratura avviene poi applicando una funzione di cifratura su ogni blocco.
Generalmente la dimensione del blocco scelta è della medesima lunghezza della chiave perché risulta semplice per l’implementazione di un algoritmo. Tuttavia è bene fare attenzione ad alcuni metodi che possono compromettere la sicurezza dell’algoritmo. Nei seguenti algoritmi individuiamo:
k è la chiave
Pi è l’i-esimo blocco del testo in chiaro
Ci è l’i-esimo blocco del testo cifrato
Electronic Code Book (ECB)
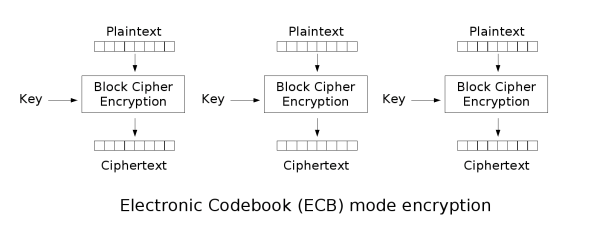
S(Pi, ki) = Ci
È l’implementazione più semplice, in cui l’unica cosa che nasconde il testo in chiaro è la chiave (o una parte di essa). Su questo metodo si basano sistemi come il cifrario di Vigenere e sappiamo che questo metodo risulta essere tanto semplice quanto insicuro. Infatti è sufficiente per l’attaccante raccogliere un numero sufficiente di campioni per poter eseguire un attacco di tipo statistico come il metoto Kasiski.
Anche per i cifrari a blocchi è possibile effettuare attacchi di questo tipo ma all’aumentare della lunghezza del blocco aumenterà anche la quantità di dati cifrati da analizzare per trovare collisioni cioè blocchi cifrati allo stesso modo. Ogni collisione mostra informazioni utili a trovare la chiave e il paradosso del compleanno ci mostra come la probabilità di ottenere due blocchi cifrati allo stesso modo cresca molto velocemente all’aumentare dei blocchi cifrati. Senza esplicitare i calcoli che sono complessi, diciamo che possiamo ritenere sicura solo la radice quadrata di tutte le combinazioni possibili. Per esempio con una dimensione di 64 bit, che genererebbe 264 possibili combinazioni, potremo impiegarne solo 232 prima di cominciare a rivelare informazioni sulla chiave.
Questa limitazione è inaccettabile poichè per manenere il sistema sicuro dovremmo o utilizzare blocchi (e chiavi!) enormi oppure trasferire pochi dati prima di dover cambiare chiave, che non è poi così diverso dall’usare una chiave enorme. Per questo motivo è necessario effettuare una diversa correzione al sistema.
Cipher Block Chaining (CBC)
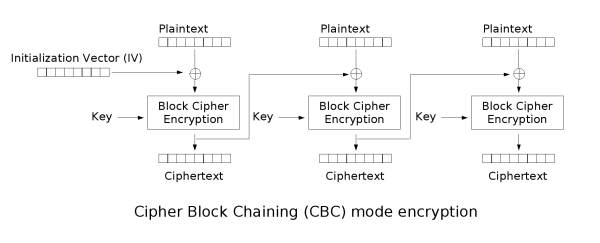
S((IV ⊕ P1, k1) = C1
S((Ci-1 ⊕ Pi, ki) = Ci
Per superare i limiti di sicurezza di ECB, è necessario l’utilizzo di una tecnica in cui lo stesso blocco di testo in chiaro, se ripetuto, produce blocchi di testo cifrato differenti nonostante sia cifrato sempre con la stessa chiave. Questo è ciò che accade con la modalità CBC, in cui l’input dell’algoritmo di crittografia è il risultato dello XOR (indicato con il simbolo ⊕) tra il blocco di testo in chiaro corrente e il blocco di testo cifrato precedente; per ciascun blocco viene utilizzata la stessa chiave.
In fase di decifratura, ciascun blocco di testo cifrato passa attraverso l’algoritmo di decrittografia; il risultato subisce uno XOR con il blocco di testo cifrato precedente, per produrre il blocco di testo in chiaro.
Per produrre il primo blocco di testo cifrato, lo XOR viene effettuato tra un vettore di inizializzazione IV (dall’inglese initialization vector) e il primo blocco di testo in chiaro. In decifratura, l’IV subisce uno XOR con l’output dell’algoritmo di decrittografia in modo da ottenere nuovamente il primo blocco di testo in chiaro.
Il vettore di inizializzazione IV deve essere dunque noto non solo al mittente ma anche al destinatario, che tipicamente lo riceve assieme alla chiave.
Esistono altri sistemi basati sullo stesso principio quali Cipher Feedback (CFB), Output Feedback (OFB) o Counter (CTR) che presentano ognuno i propri vantaggi e svantaggi. Puoi approfondire qui l’argomento.
Esempi di algoritmi
Finora è stato descritto lo schema generale di funzionamento dei cifrari a blocchi ma non sono ancora stati descritti gli algoritmi di cifratura da applicare ad ogni blocco. Di seguito sono descritti 4 algoritmi: il cifrario di Feistel, DES, triplo DES e AES.
Cifrario di Feistel
Questo cifrario, detto anche rete di Feistel, fu ideato dal crittologo Horst Feistel nel 1973; si tratta di un cifrario che mescola trasposizioni e sostituzioni a livello di bit, non di carattere. Non ha avuto di per sé applicazioni pratiche, ma è stato usato come componente fondamentale per costruire cifrari reali, il più noto di tutti è il DES.
Il testo chiaro deve essere prima di tutto tradotto in una sequenza di bit secondo un qualche codice binario, come l’ASCII. Per esempio il messaggio chiaro “Chiedo conferma” usando il codice ASCII si traduce nella seguente sequenza di bit:
| Alfabetico | C | h | i | e | d | o | c | o | n | f | e | r | m | a | |
| Binario | 01000011 | 01101000 | 01101001 | 01100101 | 01100100 | 01101111 | 00100000 | 01100011 | 01101111 | 01101110 | 01100110 | 01100101 | 01110010 | 01101101 | 01100001 |
È poi necessaria una chiave segreta K di N bit (64, 128, 256 bit o altro); per semplicità, ma senza perdere in generalità, prenderemo come esempio una chiave di soli 8 bit divisa in due sottochiavi da 4 bit: 0100 1110.
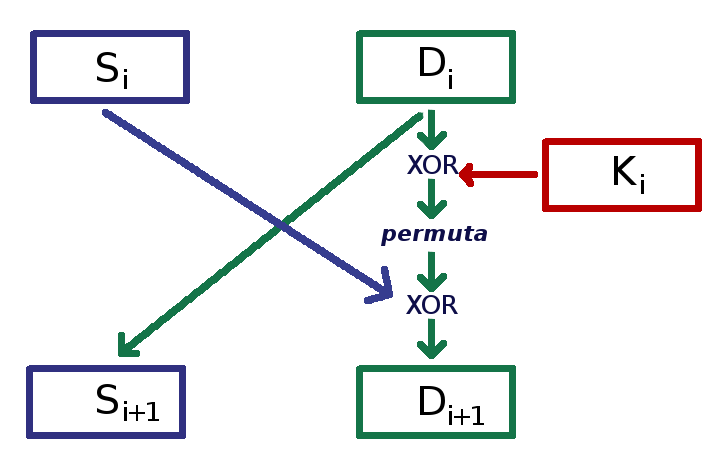
Singolo round di cifratura in una rete di Feistel

Singolo round di cifratura in una rete di Feistel
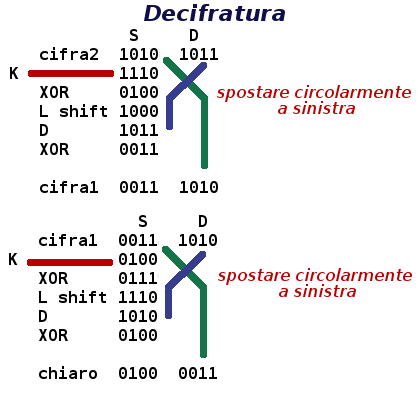
Il metodo si articola in una serie di cicli, detti round, che consistono nel dividere in due parti uguali il blocco da cifrare e nello scambiarli; uno dei due blocchi viene anche sottoposto a un misto di permutazioni e sostituzioni usando la sottochiave, come nello schema qui accanto, dove Si, Di, Ki sono i blocchi sinistro e destro e la sottochiave dell’i-esimo ciclo, Si+1, Di+1 quelli del ciclo successivo.
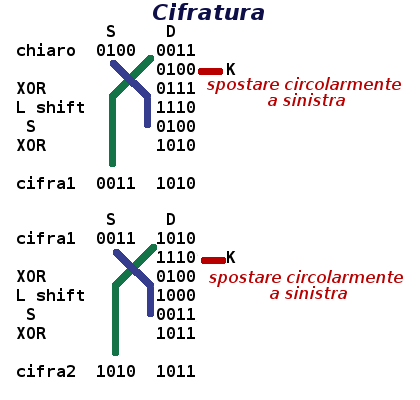
Vediamo in maggior dettaglio il metodo usando come esempio solo il primo blocco di 8 bit da cifrare: 0100 0011.
Schema di cifratura e decifratura di una rete di feistel composta da due round


Singolo round di cifratura in una rete di Feistel
Questa sequenza viene divisa in due parti uguali: sinistra S=’0100’ e destra D=’0011’.
D diventa la S del prossimo ciclo (in simboli Si+1 ← Di); la D del prossimo ciclo (Di+1)si ottiene con un misto di trasposizioni e sostituzioni: si calcola l’addizione XOR tra la sottochiave Ki e Di, il risultato viene sottoposto ad una permutazione dei bit (la funzione risultante da XOR e permuta si scrive di solito f(K, D)); nell’esempio semplificato qui sotto la permutazione consiste nello spostare circolarmente a sinistra i bit (left shift); il risultato viene poi sommato ad Si sempre con uno XOR.
Ripetendo molte volte questa trasformazione si ottiene una sequenza di bit pressochè casuale, che dovrebbe nascondere del tutto ogni caratteristica statistica del testo cifrato.
In definitiva una rete di Feistel prevede tre parametri variabili: la lunghezza della chiave K, la dimensione del blocco di bit, il numero di iterazioni del ciclo appena descritto. Inoltre va definita la funzione F(K, D).
Tanto più grandi sono questi parametri, tanto maggiore la sicurezza, ma a scapito della complessità e della velocità di esecuzione.
La decifratura avviene con la stessa procedura utilizzando le sottochiavi in ordine inverso come illustrato nella figura accanto. In sostanza l’algoritmo di decifratura è identico a quello di cifratura e questo semplifica la realizzazione del software o addirittura dell’hardware dedicato, in fondo la rete di Feistel è un semplice circuito elettronico.
La rete di Feistel è stata la base di partenza di molti sistemi di crittografia dagli anni 70 agli anni 90 poichè basato su due principi indicati da Claude Shannon, padre della teoria dell’informazine e quindi della crittografia moderna, come essenziali per un sistema di crittografia robusto: i principi di confusione e diffusione. Nel suo lavoro “La teoria della comunicazione nei sistemi crittografici” pubblicato nel 1949, Shannon definisce:
- la confusione è il fatto che la relazione tra la chiave e il testo cifrato sia quanto più complessa e non correlata possibile in modo tale che non si possa risalire ad essa a partire dal testo cifrato.
- la diffusione è la capacità dell’algoritmo di distribuire le correlazioni statistiche del testo lungo tutto l’alfabeto utilizzato dall’algoritmo di cifratura rendendo quanto più difficile possibile un attacco statistico.
La diffusione è associata alla dipendenza dei bit di uscita dai bit di ingresso. In un algoritmo con un’ottima diffusione la variazione di un bit in ingresso dovrebbe cambiare tutte le uscite con probabilità del 50%.
La sostituzione è la tecnica più utilizzata per eliminare le predominanze statistiche e quindi è il primo metodo da utilizzare per implementare una buona confusione (vedi S-box).
Puoi trovare altri dettagli qui
In realtà quella qui descritta è una funzione di feistel semplificata che non è in grado così com’è di rispettare a dovere i principi di confusione e diffusione, la permutazione infatti non dovrebbe consistere semplicemente in un left shift. Diversi crittosistemi ispirati alle reti di feistel possono implementare funzione differenti come vedremo col DES.
DES (Data Encryption Standard)
Struttura generale della rete di Feistel del DES.

Struttura generale della rete di Feistel del DES
IBM che era allora leader mondiale nella produzione di computer nel 1973 presentò Lucifer che era di fatto un’implementazione del cifrario di Feistel; Lucifer è oggi quasi dimenticato perché fu quasi subito soppiantato dal DES (Data Encryption System) che nel 1977 fu certificato dal NIST (National Institute of Standards and Technology = istituto nazionale degli standard e della tecnica degli USA), diventando l’algoritmo di cifratura più usato fino agli anni ‘90.

Trasposizione iniziale Ti e trasposizione finale Tf

Trasposizione iniziale Ti e trasposizione finale Tf
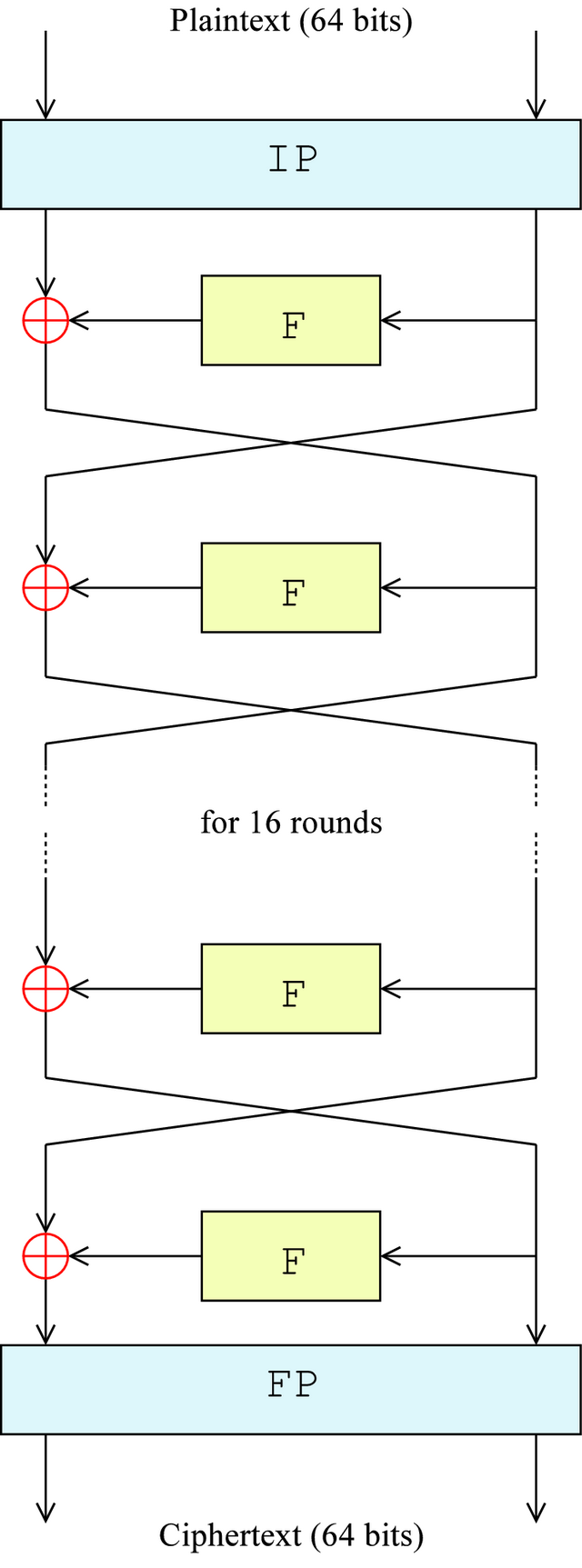
Struttura generale
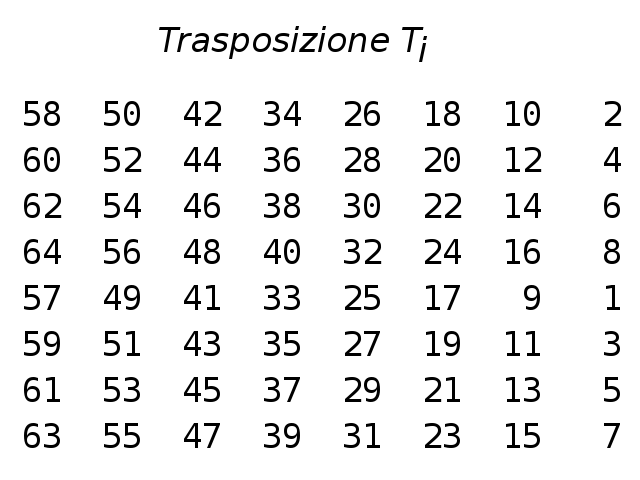
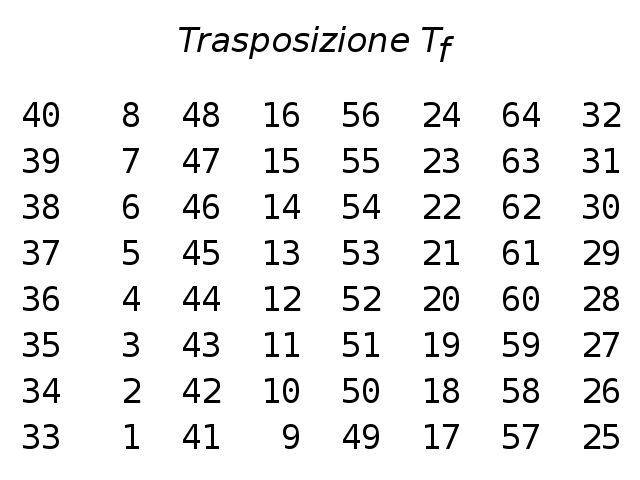
Anche DES è basato sul cifrario di Feistel e utilizza blocchi di 64 bit, chiave di 64 bit (dei quali otto di controllo, per cui in effetti la chiave è di 56 bit) e 16 cicli (round) di Feistel, ai quali si aggiungono una trasposizione iniziale ed una finale. (vedi tabelle a fianco)
In pratica il messaggio alfanumerico è rappresentato in una codifica binaria, e quindi suddiviso in blocchi B di 64 bit, mentre la chiave K è un blocco di 56 bit.
A questo punto ogni blocco viene cifrato in tre passi:
- Il blocco B è sottoposto a una trasposizione iniziale Ti (o IP, initial permutation) producendo il blocco B1;
- B1 è cifrato con 16 cicli di Feistel producendo alla fine il blocco B2;
- B2 è sottoposto alla trasposizione finale Tf (o FP, final permutation) inversa della Ti.
Nella figura a fianco il simbolo ⊕ denota l’operazione XOR e F è la funzione di Feistel (F-function) che nel paragrafo precedente era semplificata in una sequenza XOR - left shift - XOR. In questo caso, per rispettare a dovere i principi di confusione e diffusione è stata implementata una funzione più complessa.

Struttura della funzione di Feistel o F-function

Struttura della funzione di Feistel o F-function
Funzione di Feistel
La funzione Feistel, opera su mezzo blocco (32 bit) per volta e consiste di quattro passi:
- Espansione: il mezzo blocco di 32 bit è espanso fino a 48 bit utilizzando la permutazione di espansione contraddistinta con E nello schema, che duplica alcuni bit.
- Miscelazione con la chiave: il risultato è combinato con una sottochiave usando un’operazione di XOR. Sedici sottochiavi di 48 bit — una per ogni ciclo — sono derivate dalla chiave principale usando il gestore della chiave (descritto più avanti).
- Sostituzione: dopo la miscelazione con la sottochiave, il blocco viene diviso in otto parti di sei bit prima del processamento con le S-box o substitution box (“scatole di sostituzione”). Ognuna delle otto S-box sostituisce sei bit in input con quattro bit in output mediante una trasformazione non lineare effettuata attraverso una tabella. Le S-box forniscono il cuore della sicurezza del DES — senza di esse, la cifratura sarebbe lineare e quindi facilmente violabile.
- Permutazione: infine, i 32 bit risultanti dalle S-box sono riordinati in base alle permutazioni fisse della P-box o permutation box.
L’alternanza di sostituzioni mediante le S-box, le permutazioni con la P-box e le espansioni garantiscono il rispetto dei principi di confusione e diffusione.
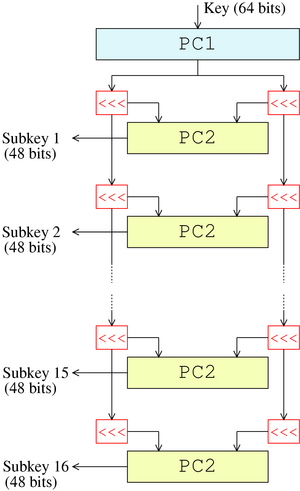
Gestore della chiave
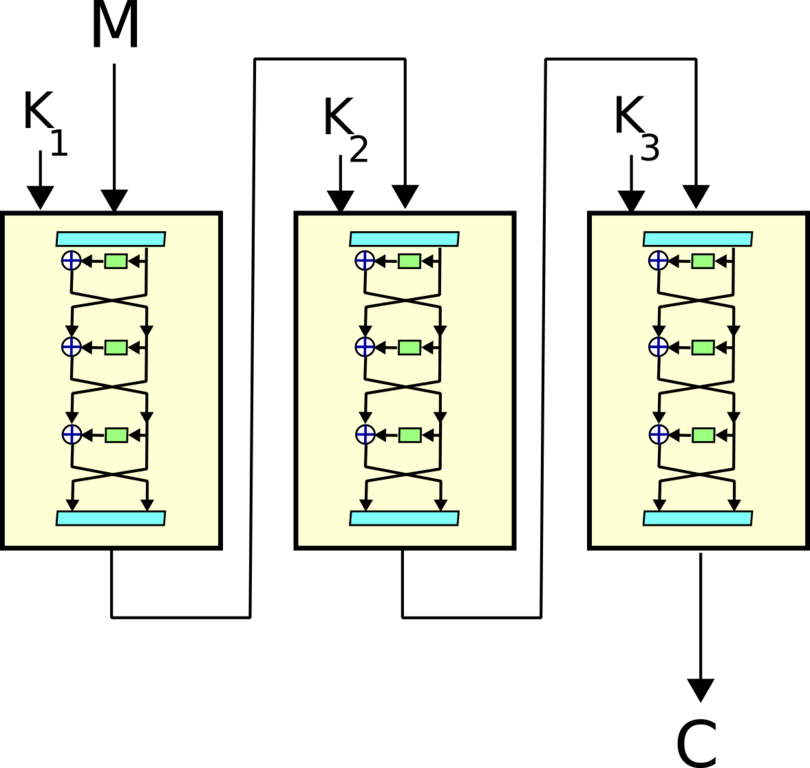
Schema generale del triplo DES

Schema generale del triplo DES
La chiave in DES ha una lunghezza di 64 bit ma in ogni round viene utilizzata una sottochiave di 48 bit che varia ad ogni round sulla base di un algoritmo. Inizialmente vengono scartati 8 bit che possono essere usati come bit di controllo della parità (PC1 nella figura). I rimanenti 56 bit vengono ad ogni round separati in due parti (28 bit ciascuna) e su ognuna di queste parti viene applicato un left shift di 1 o 2 posizioni. Dei 56 bit così modificati ad ogni round vengono scelti solo 48 bit da usare nella funzione di Feiestel secondo una apposita tabella di permutazione (PC2 nella figura, in realtà sono due una per ogni metà).
Durante la fase di decifratura il procedimento è lo stesso ma si applicano dei right shift.
Se vuoi vedere in dettaglio il funzionamento del DES puoi trovare la descrizione completa qui e gli schemi dei singoli componenti qui.
Sicurezza e crittanalisi
Nonostante siano state pubblicate più informazioni sulla crittanalisi del DES che per ogni altro algoritmo di cifratura a blocchi, il tipo più pratico di attacco a tutt’oggi è quello con forza bruta.
Nonostante il sistema su cui si basa rispetti i principi teorici di un buon sistema di crittografia, la sicurezza del DES è stata messa in discussione fin da subito; con una chiave di 56 bit le chiavi possibili sono 256 numero enorme, assolutamente fuori della portata per un essere umano, ma non di quella dei moderni computer.
In altre parole il DES non è affatto al sicuro dal più semplice degli attacchi crittanalitici, quello esaustivo (in inglese: brute-force) che semplicemente prova una per una tutte le chiavi.
Nel 1993 Wiener presentò un progetto di computer dedicato in grado di decrittare il DES, unico difetto il costo stimato in un milione di dollari! Nel 1998 un gruppo di tre aziende Cryptographic Research, Advanced wireless technologies, Electronic Frontier Foundation comunicò di aver realizzato DES Cracker una macchina per la ricerca delle chiavi dal costo di 250000 $ in grado di forzare la chiave del DES in 56 ore. Comunicazione che mostrò definitivamente che la chiave di 56 bit era troppo corta.
La fragilità del DES non risiede quindi nella natura del sistema su cui si basa, la rete di Feistel, ma nella dimensione della chiave. Il DES a 64 bit ha dovuto così cedere il passo a un DES a 128 bit e al triplo DES, Nel 2001 è stato presentato il nuovo protocollo AES destinato a sostituire progessivamente il DES.
3DES (Triple DES)
Schema generale del triplo DES
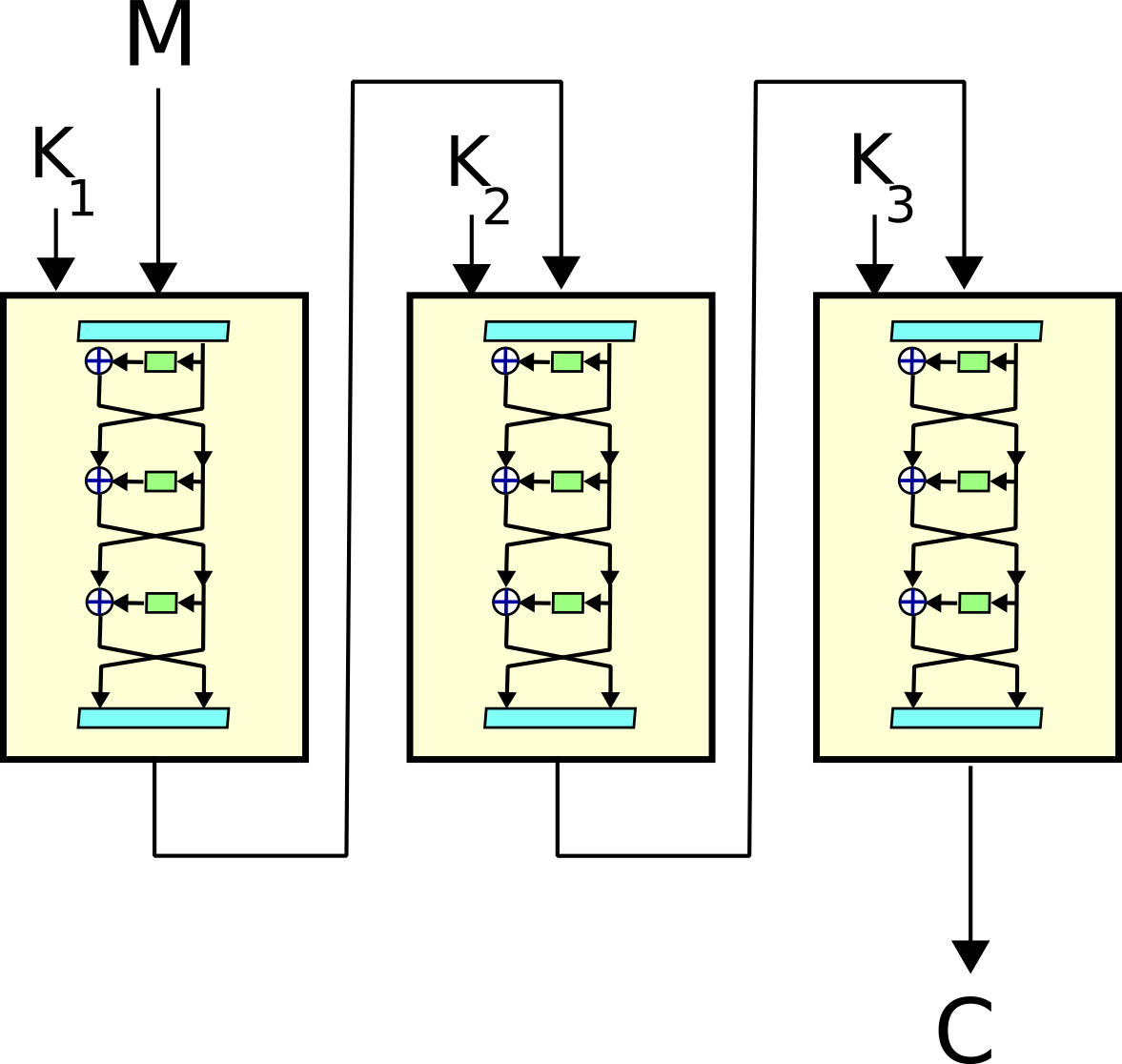
Schema generale del triplo DES
Quando DES non fu più sicuro, si cercò un metodo che mantenesse le meccaniche del DES ma che permettesse di avere una chiave più lunga. In questo algoritmo si esegue una tripla crittazione impiegando 3 chiavi DES standard, a 56 bit, ottenendo una chiave a 168 bit. È possibile anche invertire il secondo passaggio, ovvero eseguire una crittazione e una decrittazione. Tuttavia non modifica la sicurezza generale dell’algoritmo.
Anche questo algoritmo oggi non viene più impiegato poiché le tecnologie si stanno evolvendo e molti algoritmi di crittazione non risultano abbastanza forti da sopportare le elevate capacità di calcolo dei computer moderni, soprattutto con l’avvento delle GPGPU (general-purpose computing on graphics processing units ovvero le schede video dei nostri computer). 3DES ha lasciato il posto a AES, il nuovo standard ormai.
Puoi trovare altri dettagli qui
AES (Advanced Encryption Standard)
Il 2 gennaio 1997 l’americano NIST (National Institute of Standards and Technology) lanciò un concorso per un nuovo cifrario simmetrico (a chiave segreta) denominato Advanced Encryption System che potesse prendere il posto del DES e avesse una sicurezza almeno pari al Triplo DES. Dopo aver esaminato molti cifrari proposti da crittologi di tutto il mondo il 2 ottobre 2000 il NIST annunciò di aver scelto il cifrario Rijndael ([ˈrɛindaːl]) progettato da due crittologi belgi Joan Daemen e Vincent Rijmen; l’AES-Rijndael fu certificato nel 2001 come nuovo standard di cifratura. Il nome Rijndael è una sintesi dei nomi dei suoi inventori.
AES lavora su blocchi a dimensione fissa di 128 bit. Inizialmente la lunghezza standard per la chiave era di 128 bit ma è stata prevista la possibilità di impiegate chiavi più lunghe da 192 e 256 bit, cosa che con l’aumentare della potenza di calcolo disponibile risulta ormai necessario per buoni livelli di sicurenzza.
Chiave da 128 bit
| k0 | k4 | k8 | k12 |
| k1 | k5 | k9 | k13 |
| k2 | k6 | k10 | k14 |
| k3 | k7 | k11 | k15 |
Blocco da 128 bit
| b0 | b4 | b8 | b12 |
| b1 | b5 | b9 | b13 |
| b2 | b6 | b10 | b14 |
| b3 | b7 | b11 | b15 |
Come il DES, AES prevede la ripetizione di numerosi cicli identici. Per l’AES a 128 bit, sono previste 10 ripetizioni del ciclo base. Ogni blocco di 128 bit è diviso in 16 bytes, che dobbiamo immaginare disposti su una matrice 4x4.
Ogni ciclo di Rijndael è una funzione del blocco in ingresso e della chiave, che denoteremo con Round(blocco, chiave) e consiste delle seguenti 4 funzioni:
- Round(blocco, chiave)
- SubBytes(blocco): applica ad ogni byte x del blocco in entrata la trasformazione Ax-1 + b dove A e b sono una matrice e un vettore prefissati e x-1 è l’inverso moltiplicativo di x nell’aritmetica finita definita campo di Rijndael; essendo presente x-1, la funzione SubBytes() non è lineare così che non è lineare nemmeno la Round(,_) cosa importante perché mette al riparo dagli attacchi della crittanalisi differenziale.
- ShiftRows(blocco): applica al blocco in entrata uno scorrimento a sinistra (L-shift) riga per riga: la riga 0 resta invariata, la riga 1 scorre a sinistra di 1 posizione, la riga 2 di 2 posizioni, la riga 3 di 3 posizioni.
- MixColumns(blocco): ogni colonna della matrice in entrata è moltiplicata per una data matrice con lo scopo di diffondere e confondere i bit.
- AddRoundKey(blocco, chiave): effettua una semplice addizione-XOR tra i bit del blocco in ingresso e quelli della chiave.
- …
- FinalRound(blocco, chiave): l’ultimo ciclo è uguale ai precedenti, ma senza la funzione MixColumns.
La sicurezza di AES
Dal 2001 sono stati pubblicati diversi progetti di attacco ad AES basati su metodi esaustivi o nel migliore dei casi su algoritmi 4 volte più veloci degli esaustivi. I tempi richiesti per recuperare la chiave sono comunque elevatissimi; nel 2011 è stato pubblicato “Andrey Bogdanov, Dmitry Khovratovich, and Christian Rechberger (2011). Biclique Cryptanalysis of the Full AES” che richiede qualcosa come 2126. operazioni per forzare una chiave AES a 128 bit, 2190 per AES 192 bit e 2254 per AES a 256 bit.
Il livello di sicurezza di AES sembra quindi molto elevato; per i documenti del governo USA AES 128 bit è considerato sufficiente per i documenti classificati “Secret”, mentre per i “Top secret” occorre AES 192 o meglio ancora 256 bit.
Puoi trovare altri dettagli su AES qui.
Cifrari a flusso
I cifrari a flusso sono cifrari simmetrici che non lavorano su un blocco di cifre con una chiave delle stesse dimensioni, come nei cifrari visti finora, ma combino la chiave (o una sequenza di numeri da essa derivata) con l’intero messaggio, di solito attraverso operazioni XOR.
I cifrari a flusso sono ispirati al cifrario di Vernam, l’unico sistema crittografico per cui esiste la dimostrazione matematica della sua assoluta sicurezza. L’idea di questi cifrari infatti è quella di imitare l’utilizzo di una chiave lunga come l’intero messaggio, generando in fase di cifratura (e decifratura poichè simmetrico) una sequenza di numeri pseudocausali con cui cifrare il messaggio. La differenza col cifrario di Vernam è che in quel caso la chiave è davvero costituita da valori totalmente casuali e imprevedibili, caratteristica che rende il sistema sicuro; in questo caso invece la sequenza di caratteri generata è solo pseudocasuale.
Una sequenza di numeri pseudocasuale è prodotta da un algoritmo deterministico il cui stato di partenza dipende da un valore detto comunemente “seed” (seme in inglese) che costituisce in questo contesto la chiave di cifratura. Questa sequenza di numeri non è quindi davvero casuale ma dipende dalla chiave, e a una stessa chiave corrisponde sempre una stessa sequenza di numeri pseudocasuali, motivo per cui conoscendo la chiave è possibile generare la stessa sequenza sia in fase di cifratura che di decifratura. L’unica cosa in cui la sequenza assomiglia ad una realmente casuale è che produce le stesse proprietà statistiche (frequenza e distribuzione dei valori…).
Un’altra proprietà significativa di un generatore di numeri casuali è il suo periodo, ovvero il numero di elementi dopo i quali la sequenza si ripete. In generale più è lungo il periodo e migliore è la qualità del generatore. Nel nostro caso la sequenza prodotta equivarrà alla chiave realmente usata per cifrare i messaggi in chiaro e come sappiamo quando la chiave si ripete è possibile effettuare un attacco.
RC4
Un esempio di implementazione particolarmente famoso ed utilizzato in passato di questo sistema è l’algoritmo RC4 che consiste nella generazione di un flusso di bit pseudocasuale (keystream) combinato mediante un’operazione di XOR con il testo in chiaro per ottenere il testo cifrato. L’operazione di decifratura avviene nella stessa maniera, passando in input il testo cifrato ed ottenendo in output il testo in chiaro, questo perché il keystream è lo stesso a partire dalla stessa chiave e lo XOR è un’operazione simmetrica.
Non ci interessa approfondire i dettagli tecnici riguardo a questo algoritmo che puoi approfondire qui, quello che ci interessa analizzare è come algoritmi quali RC4 paghino la propria semplicità e velocità in termini di sicurezza: questa infatti è molto debole e l’algoritmo è violabile con relativa facilità e velocità, tanto che il suo uso non è più consigliabile.
La debolezza di questi algoritmi risiede proprio nel legame che c’è tra la chiave e il keystream che non è una sequenza di numeri realmente casuali ma una sequenza di numeri prodotta da un algoritmo deterministico. Nel 2005 infatti è stato trovato un modo per violare una connessione wireless protetta con WEP, protocollo di cifratura per le reti Wi-Fi che usa RC4, in meno di un minuto.
Lunghezza delle chiavi nella crittografia simmetrica
Il governo statunitense impose un serio limite all’esportazione e all’utilizzo di chiavi lunghe. Per molti anni il limite imposto dal governo fu di 40 bit, che per lo standard moderni è un limite ridicolo dato che un semplice computer è in grado in poche ore di verificare tutto lo spazio delle chiavi. Infatti mentre in Europa e nel resto del mondo si diffondevano algoritmi con chiavi lunghe gli Stati Uniti d’America per via di scelte politiche rimanevano costretti a utilizzare chiavi corte. Con la diffusione di internet e del commercio elettronico il Governo degli Stati Uniti fu costretto a cambiare la legge innalzando il limite a 128 bit.
Quando nel 1977 il Data Encryption Standard (DES) venne distribuito dal governo Statunitense la lunghezza della chiave di 56 bit era più che sufficiente, sebbene nel Lucifer, predecessore del DES la chiave fosse già di 112 bit. Ma l’NSA quando approvò il DES decise di ridurre la chiave. Visto che l’NSA è una delle agenzie meglio finanziate dal governo statunitense, si ritiene che già verso la fine degli anni settanta avessero risorse tecnologiche e finanziarie sufficienti per sviluppare una macchina specializzata che forzasse il DES verificando l’intero spazio delle chiavi. Comunque negli anni novanta si dimostrò che il DES era forzabile in un paio di giorni utilizzando macchine specializzate dal costo inferiore al milione di dollari e quindi con costi accessibili a tutte le multinazionali e ovviamente a tutti i Governi. Nel libro Cracking DES (O’Reilly and Associates) viene descritto come la EFF abbia finanziato e costruito una macchina in grado di forzare il DES. Da allora sono sorti anche dei progetti basati su computer distribuito che hanno consentito di forzare chiavi a 56 bit e che attualmente stanno forzando un messaggio a 64 bit codificato con l’algoritmo RC5.
L’algoritmo Skipjack dell’NSA utilizzato dal programma Fortezza utilizza chiavi a 80 bit.
Il DES è stato temporaneamente sostituito dal Triple DES che usa tre chiavi da 56 bit per ottenere una cifratura a 168 bit.
L’Advanced Encryption Standard pubblicato nel 2001 utilizza chiavi da almeno 128 bit e è un grado di utilizzare anche chiavi a 192 o 256 bit. La chiave a 128 bit viene considerata sufficiente per compiti normali mentre l’NSA specifica che per documenti Top secret la chiave deve essere di 192 o 256 bit.
Nel 2003 l’U.S. National Institute for Standards and Technology, NIST, ha proposto di abbandonare tutte le chiavi a 80 bit entro il 2015.
Crittografia asimmetrica
Fino agli anni 1970 gli unici sistemi crittografici esistenti erano simmetrici cioè prevedevano l’utilizzo di un’unica chiave utilizzata sia per cifrare che per decifrare. Per quanto i crittosistemi fossero sicuri ed efficienti rimaneva da risolvere un problema fondamentale, quello della condivisione della chiave. A questo scopo vennero proposte una serie di tecniche che si possono definire di cirittocrafia asimmetrica.
Nel 1970 in ambito accademico e militare iniziò a circolare l’idea di creare un sistema di crittografia a base pubblica che superasse il problema dello scambio delle chiavi ma per qualche anno nessuno fu in grado di trovare un sistema per implementarlo. Sebbene segretamente, nel 1973, in ambito militare, si fosse già arrivati a sviluppare un sistema di cifratura a chiave pubblica analogo a RSA, fu solo nel 1974 che venne pubblicato l’algoritmo di Diffie-Hellman, il primo sistema per risolvere il proglema dello scambio delle chiavi.
Il modo migliore per capire come si sia potuti arrivare a concepire e a realizzare un sistema crittografico che non necessiti di uno scambio preventivo di chiavi da parte di mittente e destinatario è partire da un esempio. Supponiamo che, per scambiarsi documenti riservati, mittente e destinatario utilizzino una scatola alla quale sia possibile applicare due lucchetti; è dunque possibile procedere nel seguente modo:
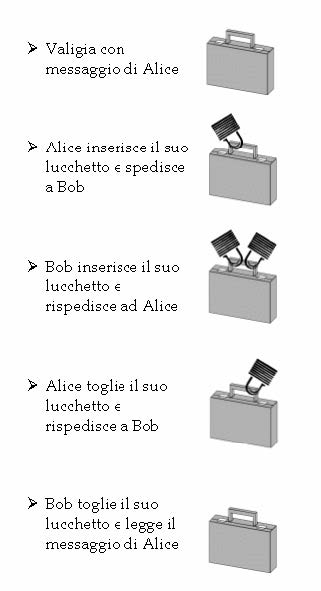

Il metodo del doppio lucchetto.
-
il mittente racchiude il messaggio nella scatola e la chiude con il lucchetto del quale solo lui possiede la chiave e spedisce la scatola al destinatario;
-
il destinatario riceve la scatola ma non può aprirla dato che non ha la chiave del lucchetto; applica a questo punto un altro lucchetto, del quale solo lui possiede la chiave e rimanda la scatola al mittente;
-
il mittente alla ricezione della scatola toglie il lucchetto che aveva precedentemente applicato e la rispedisce al destinatario;
-
la scatola che arriva al destinatario è ormai chiusa solo con il lucchetto da lui stesso applicato: egli, quindi, potrà aprirla senza problemi e leggere il messaggio in essa racchiuso, senza che nessun terzo incomodo possa averne sbirciato il contenuto.
Questa idea però non è immediatamente traducibile in un modello matematico, in quanto: svolgere il primo passaggio (mettere il primo lucchetto alla scatola) significa partire da certi dati iniziali (scatola senza lucchetti), applicare ad essi una determinata funzione matematica (primo lucchetto) e raggiungere un certo risultato (scatola con un lucchetto); svolgere il secondo passaggio (mettere il secondo lucchetto alla scatola) significa partire dai risultati del primo passaggio (scatola con un lucchetto), applicare ad essi una diversa funzione matematica (secondo lucchetto) e raggiungere un altro risultato (scatola con due lucchetti); il terzo passaggio consiste nell’inversione della funzione utilizzata nel primo passaggio (cioè nel togliere il primo lucchetto messo); il quarto, ovviamente, si realizza invertendo la funzione applicata nel secondo passaggio. Ma in questo modo non si riottengono, in generale, i dati iniziali (scatola senza lucchetto) poiché l’inversione della composizione di due funzioni deve avvenire in ordine contrario rispetto all’ordine di applicazione, cioè va invertita per prima quella applicata per ultima.
Tutto ciò risulta evidente dall’esempio che segue.
Esempio
Chiave di Alice
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| H | F | S | U | G | T | A | K | V | D | E | O | Y | J | B | P | N | X | W | C | Q | R | I | M | Z | L |
Chiave di Bob
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| C | P | M | G | A | T | N | O | J | E | F | W | I | Q | B | U | R | Y | H | X | S | D | Z | K | L | V |
| MESSAGGIO: | ci vediamo | |
| Cifrato da Alice: | SV RGUVHYB | |
| Ricifrato da Bob: | HD YNSDOLP | |
| Decifrato da Alice: | AJ MQCJLZP | |
| Decifrato da Bob: | EI CNAIYWB | che non è “ci vediamo” |
Questo problema fu affrontato e risolto nel 1976 dai ricercatori Whitfield Diffie, Martin Hellman e Ralph Merkle i quali si servirono dell’algebra dei moduli dove spesso è possibile incontrare funzioni unidirezionali o difficilmente invertibili cioè funzioni agevoli da calcolare in una direzione ma che diventano computazionalmente intrattabili nella direzione opposta (funzione inversa). Dall’idea dei tre ricercatori sono seguiti poi altri sistemi più complessi. Per poter comprendere come funzionano questi sistemi è necessario studiare la matematica che ne sta alla base.
La matematica alla base della crittografia asimmetrica
Tutti i sistemi di crittografia asimmetrica sono basati su due concetti matematici fondamentali: i numeri primi e l’aritmetica dei moduli.
Numeri primi
Un intero positivo N si dice primo se
N è diverso da 1 ed è divisibile esattamente solo per 1 e per se stesso.
Ancora oggi il metodo più veloce per trovare tutti i numeri primi inferiori ad un limite L prefissato è il crivello di Eratostene. Tale algoritmo può essere schematizzato con i seguenti punti:
- si costruisce un elenco E degli interi compresi tra 2 e L;
- si cancellano tutti i multipli di 2 tranne 2;
- si prende il primo numero non cancellato, che è 3, e si cancellano tutti i suoi multipli (escluso lui stesso);
- si continua così fino alla parte intera della radice quadrata di L. I numeri superstiti sono i numeri primi compresi tra 2 e L.
Chi lo desidera può vedere il crivello in azione qui.
Il Teorema Fondamentale dell’Aritmetica stabilisce che:
ogni numero intero diverso da 0,-1,+1 si decompone nel prodotto di numeri primi e la decomposizione è unica a meno dell’ordine e del segno dei fattori.
Dal Secondo Teorema di Euclide sui numeri primi sappiamo che i numeri primi formano una successione infinita.
È da notare che la dimostrazione di Euclide della esistenza di infiniti numeri primi è costruttiva, fornisce cioè un metodo che consente, almeno in linea di principio, di trovare un numero primo che sia al di fuori di qualsiasi insieme finito Q di numeri primi assegnato!
La tecnica è la seguente:
- Sia Q = {q1 , q2 , q3 ,…, qm};
- si calcola n = q1 · q2 · q3 · … · qm + 1 ;
- evidentemente n è coprimo con tutti i qj contenuti in Q (cioè non ha fattori in comune con essi): quindi, tutti i suoi fattori primi sono primi che non stanno in Q.
Esempio Supponiamo di conoscere soltanto i numeri primi 2 e 3.
Allora Q = {2, 3}, n = 2 · 3 + 1 = 7 , che è primo.
Si aggiunge 7 a Q e si ottiene Q = {2, 3, 7}.
Al passo seguente si ha n = 2 · 3 · 7 + 1 = 43 , che è primo anch’esso.
Lo aggiungo al bottino: Q = {2, 3, 7, 43}.
Si prosegue in questo modo: n = 2 · 3 · 7 · 43 + 1 = 1806 che può essere scomposto in fattori primi come 1806 = 13 · 139 , aggiungendo quindi due nuovi numeri all’insieme Q che diventa Q = {2, 3, 7, 43, 13, 139}.
Denotiamo la successione dei primi in ordine ascendente con p1 , p2 ,…, pn.
Avremo allora: p1 = 2, p2 = 3, p3 = 5, …
E inoltre: p10 = 29, p100 = 541, p1000 = 7979, p10000 = 104709
Una funzione di importanza fondamentale è la funzione enumerativa dei numeri primi indicata con π(x):
\(\pi(x)\) = numero dei primi minori o uguali a x
Si ha quindi: π(10) = 4 perché ci sono 4 primi (2,3,5,7) minori di 10.
Alcuni valori di π(x) sono:
π(100) = 25
π(1000) = 168
π(10000) = 1229
π(100000) = 9592
π(1000000) = 78498
π(10000000) = 664579
Sulla pagina in inglese di wikipedia dedicata alla funzione π sono riportati valori calcolati e stimati della funzione. Il più grande che possiamo trovare, pubblicato da David Baugh and Kim Walisch nel 2015 è:
π(1027) = 16,352,460,426,841,680,446,427,399
Calcolare il valore esatto della funzione π(n) per valori così grandi di n richiede una quantità di calcoli inimmaginabile. Fortunatamente è possibile calcolare un valore approssimato di π(n) per mezzo del Teorema dei numeri primi il quale afferma che:
Tra le altre, una conseguenza del teorema dei numeri primi è che la probabilità che un numero x preso a caso sia primo è circa:
Esempio La probabilità che un intero casuale di 1000 cifre sia primo è circa 1 / log(101000). Tenendo presente che nel Teorema dei numeri primi il logaritmo è in base e: log(101000) = 1000 · log(10) = 2302,59. Quindi, in media, troveremo un numero primo ogni 2302 interi presi a caso.
E’ possibile, dato un intero x casuale, provare velocemente che x è primo?
Naturalmente esiste un metodo ovvio (di forza bruta): dividerlo per gli interi che lo precedono. Oppure, cosa assai più intelligente, mettere in moto un crivello di Eratostene. Entrambi però richiederebbero tempi proibitivi di calcolo anche con numeri di modesta lunghezza, persino utilizzando supercomputers.
Accenniamo qui soltanto al fatto che esistono metodi per dimostrare che un interno è probabilmente primo, con una probabilità di errore che si può rendere piccola a piacere (tra questi ricordiamo il Test di Fermat). Esistono poi anche metodi molto più efficaci, per i quali la probabilità di errore è ancora più bassa. Il punto di forza di tutti questi metodi è che il tempo che impiegano ad eseguire il test su x è polinomiale, cioè è esprimibile mediante un polinomio nel numero delle cifre di x. Nel 2002 tre ricercatori indiani (Agrawal, Saxena e Cayal) hanno trovato un algoritmo che è al tempo stesso polinomiale e deterministico per dimostrare la primalità di un numero.
Questo è un grande risultato, che ha risolto una congettura rimasta aperta per decenni. Il loro algoritmo però non è ancora utilizzato in pratica, perché è molto più lento dei test probabilistici, i quali, del resto, sono quasi certi per i primi di centinaia di cifre che servono attualmente in crittografia.
Aritmetica modulo n
Nel seguito N e Z denoteranno rispettivamente l’insieme dei numeri naturali {0,1,2,…} e l’insieme degli interi relativi {…,-2,-1,0,+1,+2,…}. Dati a, b in Z ed n > 1 in N, diciamo che a è congruo a b modulo n se a e b divisi per n danno lo stesso resto; in questo caso scriviamo una relazione di equivalenza. a ≡ b mod(n). La relazione di congruenza è una relazione di equivalenza.
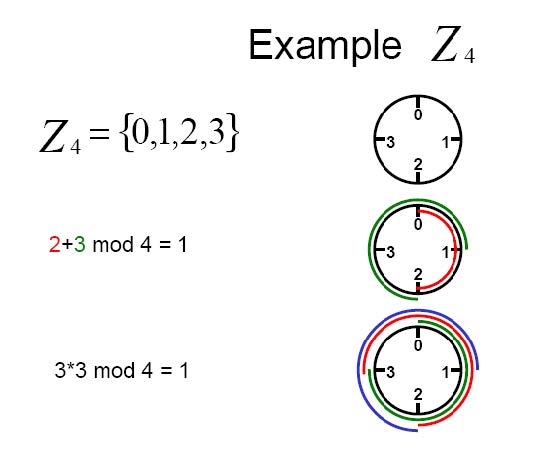
Esempio L’aritmetica dei moduli prende in considerazione un gruppo limitato di numeri disposti ad anello, un po’ come le ore sul quadrante dell’orologio.
Consideriamo ad esempio un quadrante contenente solo 7 numeri, da 0 a 6, corrispondente al modulo 7.
Per calcolare 2 + 3 si partirà da 2 e ci si sposterà di 3 numeri, ottenendo 5. Per calcolare 2 + 6 si partirà da 2 e ci si sposterà di 6 numeri. In questo modo, attraversando l’intero anello, si otterrà come risultato 1.
In pratica:
2 + 3 ≡ 5 mod(7)
2 + 6 ≡ 1 mod(7)
Ovviamente a ≡ b mod(n) se e solo se a = n · b + k con k in Z.
Per indicare tutti i numeri che differiscono tra di loro per un multiplo di n si usa il nome classe di resto modulo n (insieme di numeri che hanno in comune il resto della divisione per n).
Tali classi sono indicate usando tale resto con una sopralineatura:
- 0 classe di resto modulo 0: insieme dei numeri interi che divisi per n danno 0;
- 1 classe di resto modulo 1: insieme dei numeri interi che divisi per n danno 1;
- …
- n-1 classe di resto modulo n-1: insieme dei numeri interi che divisi per n danno n-1;
Si indica con Zn l’insieme delle classi di resto modulo n: Zn = {0, 1, …, n-1}.
Sono valide le seguenti proprietà:
a + b = a + b
a · b = a · b
Esempio
Operazioni in Z5

Il cifrario di Cesare “generalizzato” con l’aritmetica modulo n
Precedentemente abbiamo parlato del cifrario di Cesare e di come fosse possibile generare messaggi cifrati per mezzo di questo metodo. Vedremo ora come sia possibile generalizzare tale sistema di cifratura utilizzando le classi di resto, e ottenendo così una cifratura che non trasla soltanto le lettere dell’alfabeto, ma le “rimescola”.
Consideriamo l’insieme delle classi di resto modulo 26, e associamo ad ogni lettera dell’alfabeto una classe di resto modulo 26. Fissiamo due numeri, detti parametri di cifratura, e otteniamo la lettera che sostituirà la lettera indicata dalla classe x con quella individuata dalla classe y per mezzo della formula:
y = a · x + b
Esempio
| CHIARO | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |
| y=5·x+1 | 6 | 11 | 16 | 21 | 0 | 5 | 10 | 15 | 20 | 25 | 4 | 9 | 14 | 19 | 24 | 3 | 8 | 13 | 18 | 23 | 2 | 7 | 12 | 17 | 22 | 1 |
| CIFRATO | F | K | P | U | Z | E | J | O | T | Y | D | I | N | S | X | C | H | M | R | W | B | G | L | Q | V | A |
Testo chiaro: veni, vidi, vici
Testo cifrato: gzst, gtut, gtpt
Risulta evidente che non tutte le scelte dei numeri a e b possono portare a una corretta cifratura e decifratura del messaggio: in particolare, è necessario che ogni lettera dell’alfabeto chiaro sia cifrata con una lettera differente, per evitare ambiguità nell’operazione di decrittazione.
Si può dimostrare che, per avere una “buona” chiave di cifratura, occorre scegliere a in modo tale che a abbia inverso in Z26.
Identità di Bézout
Se d = MCD(a, b) allora esistono degli interi x e y tali che d = a · x + b · y
Funzione e Teorema di Eulero
La funzione di Eulero \(\phi\)(n) indica il numero di elementi invertibile in Zn, e può essere anche interpretato come il numero di interi minori di n e relativamente primi con esso. Poiché contare le classi invertibili in Zn è come contare i numeri tra 1 e n-1 che sono coprimi con n, si può affermare che:
se n = p è primo, si ha \(\phi\)(p) = *p - 1
Si ha inoltre:
se n = pr con p primo, si ha \(\phi\)(n) = \(\phi\)(pr) = pr-1 · (p - 1)
se n = p1r1 · … · pkrk con p1,…, pk primi diversi tra loro, si ha
\(\phi\)(n) = p1r1-1 (p1-1) … pkrk-1 (pk-1)
La funzione di Eulero è alla base dell’importantissimo Teorema di Eulero:
Siano a e n due numeri interi positivi primi tra loro. Allora:
a\(\phi\)(n) ≡ 1 mod(n)
Un’applicazione della funzione di Eulero
Vedremo ora un’interessante applicazione del Teorema di Eulero, che permette di calcolare, dato un numero in forma di potenza, le cifre decimali del numero stesso scritto in forma posizionale.
Partiamo da un caso semplice per chiarire meglio il concetto: supponiamo di voler conoscere la cifra x che indica in numero di unità del numero 135. In questo caso, una semplice calcolatrice portatile consente di ottenere il risultato 371293 e scoprire così che la cifra cercata è 3.
Vediamo come si sarebbe potuto ottenere lo stesso risultato con la funzione e il teorema di Eulero: cercare la cifra che indica il numero di unità di 135 equivale a calcolare il resto della divisione per 10, ossia il numero compreso tra 0 e 9 tale che x = 135 in Z10.
-
13 ≡ 3 mod(10), in quanto il resto della divisione per 10 è uguale e pari a 3;
-
x = 135 = 35
-
per il Teorema di Eulero avremo: a = 3; n = 10; \(\phi\)(10) = \(\phi\)(2 · 5) = (2 - 1) · (5 - 1) = 4
-
3\(\phi\)(10) = 34 ≡ 1 mod(10) (infatti: 34 = 81 ≡ 1 mod(10))
-
x = 35 = 34 · 3 = 14 · 3 = 3
La cifra finale (il numero di unità) di 135 è quindi 3, come risultava dal calcolo diretto.
Esempio Si vogliono calcolare le ultime due cifre decimali (decine e unità) del numero 203327.
Le ultime due cifre decimali corrispondono al resto della divisione per 100.
Si procede quindi nel seguente modo:
- 203 ≡ 3 mod(100)
- x = 203327 = 3327
- a = 3; n = 100; \(\phi\)(100) = \(\phi\)(22 · 52) = 22-1 · (2 - 1) · 52-1 · (5 - 1) = 40
quindi: 340 ≡ 1 mod(100) - 3327 = 38·40+7 = (340)8 · 37 = 1 · 37 = 2187 = 87
Lo scambio di chiavi secondo Diffie e Hellman
Nel 1976 i ricercatori Whitfield Diffie e Martin Hellman, influenzati dal lavoro di Ralph Merkle, pubblicarono il primo sistema noto per risolvere il problema dello scambio delle chiavi. Le funzioni di cui si servirono derivano dall’aritmetica dei moduli dove è spesso possibile incontrare funzioni unidirezionali, cioè funzioni agevoli da calcolare in una direzione ma che diventano computazionalmente intrattabili nella direzione opposta (funzione inversa).
La funzione unidirezionale che fu scelta dai tre ricercatori era del tipo:
Yx mod(p)
Dove p è un numero primo e Y è un generatore ossia un numero che elevato a potenza possa generare tutti i numeri che sono primi con p, e siccome p è primo allora Y genera tutti i numeri minori di p. Chiaramente Y deve essere minore di p.
Prendiamo ad esempio due valori Y = 5 e p = 3. Dalla tabella che segue sono riportati i valori calcolati con la normale funzione esponenziale e con l’esponenziale in algebra modulare.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 3x | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 3x mod(5) | 3 | 4 | 2 | 1 | 3 | 4 | 2 | 1 | 3 | 4 |
Notiamo per prima cosa che i due numeri sono stati scelti correttamente infatti 5 è primo e 3 è un generatore in modulo 5 poichè genera tutti i numeri da 1 a 4.
Inoltre, dalla tabella si evince come in aritmetica normale sia immediato, dato un valore di x, ricavare il corrispondente valore della funzione, e viceversa, dato il valore della funzione ricavare x. In aritmetica dei moduli è altrettanto facile effettuare la funzione diretta ma risulta problematico effettuare l’operazione inversa, come ad esempio ottenere il valore di x in 3x mod(5) = 4, x potrebbe valere 2 oppure 6 o 10 o un’infinità di altri valori.
In questo caso potrebbe sembrare possibile cercare il valore di x andando per tentativi poichè i numeri generati, i numeri da 1 a 4 sono pochi, ma questo solo perchè i valori scelti 3 e 5 sono molto piccoli. Nelle applicazioni reali i numeri scelti sono numeri primi di migliaia di bit e in quei casi il calcolo del logaritmo discreto (il logaritmo nell’algebra dei moduli) risulta computazionalmente intrattabile.
Per capire effettivamente come l’algoritmo proposto da Diffie e Hellman consenta a mittente e destinatario di stabilire una chiave segreta senza incontrarsi faremo ricorso a tre persone immaginarie che chiameremo Alice (mittente), Bob (destinatario) e Eva (una terza persona che vuole spiare le conversazioni tra Alice e Bob).
Il metodo prevede che Alice e Bob concordino una chiave costituita dai numeri Y e p: l’aspetto affascinante del metodo è che Alice e Bob possono stabilire tali numeri “alla luce del sole”, senza cioè preoccuparsi di tenerli segreti (per esempio ad Eva).
Supponiamo che Alice e Bob abbiano deciso di utilizzare: Y = 13, p = 23 e vediamo con uno schema come possono procedere per stabilire senza incontrarsi una chiave che rimarrà nota solo a loro due.
| ALICE | BOB | |
|---|---|---|
| Passo 1 | Sceglie un numero che chiameremo A e lo tiene segreto, supponiamo A = 8 | Sceglie un numero che chiameremo B e lo tiene segreto, supponiamo B = 5 |
| Passo 2 | Calcola: α = YA mod(p) 138 mod(23) = 815730721 mod(23) = 2 α = 2 | Calcola: β = YB mod(p) 135 mod(23) = 371293 mod(23) = 4 β = 4 |
| Passo 3 | Alice comunica a Bob il valore di α | Bob comunica ad Alice il valore di β |
| Lo scambio di queste informazioni può avvenire tranquillamente in chiaro, in quanto un’eventuale intercettazione da parte di Eva non potrebbe comunque consentirle di risalire alla decifratura dei messaggi. Questo perché α e β NON sono la chiave, e quindi è irrilevante che Eva ne venga a conoscenza. | ||
| Passo 4 | Calcola: K = βA mod(p) 48 mod(23) = 65536 mod(23) = 9 K = 9 | Calcola: K = αB mod(p) 25 mod(23) = 32 mod(23) = 9 K = 9 |
| Chiave | Alice e Bob hanno ottenuto lo stesso numero K che rappresenterà la chiave dei loro messaggi. K = Ka = Kb = YA·B mod(p) = YB·A mod(p) = 138·5 mod (23) = 9 | |
In base a questo schema abbiamo dunque dimostrato che Alice e Bob possono concordare una chiave senza bisogno di incontrarsi e senza il timore che la chiave stessa sia intercettata da terzi: abbiamo quindi risolto il problema della distribuzione delle chiavi!
Per convincercene ulteriormente, vediamo perché ad Eva sia impossibile risalire al valore della chiave. Poiché tutte le comunicazioni dello schema precedente tra Alice e Bob sono in chiaro, Eva potrebbe aver intercettato le seguenti informazioni:
- le comunicazioni relative alla scelta di Y e p, e quindi sapere che la funzione è del tipo: 13x mod(23);
- le comunicazioni del passo 3, e quindi i valori di α e β.
Per trovare la chiave, Eva dovrebbe quindi procedere come Alice ed effettuare l’operazione βA mod(p), oppure come Bob ed effettuare l’operazione αB mod(p). Ma Eva non conosce i valori di A o di B! D’altronde, tentare di ricavarli invertendo la funzione non sarebbe un compito semplice, in quanto si tratta di una funzione unidirezionale.
Se confrontiamo l’idea originale del doppio lucchetto con la soluzione trovata notiamo che mentre quell’idea cercava di proporre un vero e proprio sistema di cifratura per trasmettere messaggi cifrati, questo sistema permette solamente di concordare un numero segreto.
La dimostrazione pubblica della loro scoperta fu data da Diffie e Hellman nel giugno del 1976 alla National Computer Conference.
L’introduzione di un metodo che consente a mittente e destinatario di scambiarsi la chiave in modo “sicuro” ha costituito una vera e proprio rivoluzione nel campo della crittografia; l’unico aspetto negativo del sistema Diffie-Hellman risiede nell’introdurre una non contemporaneità tra le azioni di destinatario e mittente. Infatti, per applicare il suo “lucchetto” Bob deve attendere di ricevere il messaggio di Alice (supponiamo tramite mail), e la stessa Alice, per rimuovere il suo “lucchetto” deve attendere la risposta di Bob, e così via. Questo aspetto, che per persone che vivono in luoghi con fusi orari differenti può comportare un “ritardo” anche notevole nello scambio delle mail, rappresenta chiaramente un elemento che va contro la natura stessa della posta elettronica, che rappresenta uno dei modi più veloci di scambio delle informazioni. Detto in termini più tecnici questo sistema è adatto solo a comunicazioni di tipo sincrono e non a comunicazioni di tipo asincrono.
Ricapitolando quindi possiamo dire che il sistema Diffie-Hellman risolve il problema della condivisione della chiave ma non offre un vero e proprio sistema di cifratura, inoltre è adatto solo a comunicazioni sincrone. Nel prossimo paragrafo vedremo come queste limitazioni siano state superate dall’introduzione della crittografia a chiave pubblica.
RSA
Il passo avanti rispetto al metodo di scambio delle chiavi secondo Diffie-Hellman avvenne grazie allo sforzo congiunto di tre ricercatori: Ronald Rivest, Adi Shamir e Leonard Adleman, dalle cui iniziali deriva il metodo noto come RSA.
Il pregio di questo sistema rispetto al metodo Diffie-Hellman è che non richiede uno scambio di informazioni tra Alice e Bob per la costruzione della chiave: questo sistema fa infatti uso di due chiavi, una detta “chiave pubblica ” e una chiamata “chiave privata” e utilizza un metodo di cifratura asimmetrico.
In un sistema a chiave asimmetrica la chiave usata per cifrare e quella usata per decifrare non coincidono: è possibile quindi che Alice renda pubblica la chiave da usare per cifrare un messaggio (la sua chiave pubblica) e conservi segreta la chiave da usare per decifrare il messaggio (la sua chiave privata), per essere in grado solo lei di decifrare i messaggi a lei diretti.
Il sistema RSA parte dall’intuizione di Diffie e Hellman di usare gli esponenziali in algebra modulare come funzione unidirezionale per arrivare ad un sistema matematico molto più complesso, che si basa per il suo funzionamento su: funzione e teorema di di eulero, piccolo teorema di fermat, teorema cinese del resto e fa affidamento sulla difficoltà della fattorizzazione di numeri molto grandi per la sua sicurezza.
Funzionamento
Il funzionamento del metodo RSA si può schematizzare con i seguenti punti:
- si scelgono due numeri primi, p e q ;
- si calcola il loro prodotto N = p · q , chiamato modulo (dato che tutta l’aritmetica seguente è in modulo n
- si sceglie poi un numero e (chiamato esponente pubblico), più piccolo di N e primo rispetto a \({\phi(N) = (p-1)\cdot(q-1)}\), dove \({\phi}\) è la funzione di Eulero;
- si calcola il numero d (chiamato esponente privato) tale che e · d ≡ 1 mod((p-1)·(q-1))
La chiave pubblica è rappresentata dalla coppia di numeri (N, e), mentre la chiave privata è rappresentata da (N, d).
Un messaggio m viene cifrato attraverso l’operazione me mod(N), mentre il messaggio c così ottenuto viene decifrato con cd = me·d = m1 mod(N). Il procedimento funziona solo se la chiave e utilizzata per cifrare e la chiave d utilizzata per decifrare sono legate tra loro dalla relazione e · d ≡ 1 mod((p-1)·(q-1)), e quindi quando un messaggio viene cifrato con una delle due chiavi (la chiave pubblica) può essere decifrato solo utilizzando l’altra (la chiave privata).
Dimostrazione matematica
La decifratura del messaggio è assicurata grazie ad alcuni teoremi matematici; infatti dal calcolo si ottiene:
\[c^d \pmod{N} = (m^e)^d \pmod{N} = m^{e·d} \pmod{N}\]Ma sappiamo che
\[e·d ≡ 1 \pmod{(p-1)·(q-1)}\]di conseguenza abbiamo che
\[e · d ≡ 1 \pmod{p-1}, \qquad e · d ≡ 1 \pmod{q-1}\]quindi, per il piccolo teorema di Fermat:
\[m^{e · d} ≡ m \pmod{p}, \qquad m^{e · d} ≡ m \pmod{q}\]Siccome p e q sono numeri diversi e primi, possiamo applicare il teorema cinese del resto, ottenendo che
\[m^{e · d} ≡ m \pmod{p · q}\]e quindi che
\[c^{d} ≡ m \pmod{N}\]Esempio di utilizzo (singola cifratura)
Vediamo in pratica come sia possibile realizzare una cifratura RSA.
Per cifrare un messaggio, questo deve essere prima di tutto trasformato in un numero o in una serie di numeri, diciamo m1, m2,…, mk. Questa operazione può essere effettuata utilizzando, ad esempio, il codice ASCII, e trasformando il numero binario ottenuto nel corrispondente in base dieci. Per semplicità, nel prossimo esempio considereremo che il messaggio segreto che si vuole trasmettere consista di un solo numero m, senza preoccuparci del metodo utilizzato per generarlo.
Faremo inoltre nuovamente riferimento ai nostri personaggi immaginari, Alice e Bob.
Operazioni effettuate da Alice (Generazione delle Chiavi):
- sceglie due numeri primi p e q:
p = 47, q = 71
- calcola N = p · q:
p = 47, q = 71
- calcola \(\phi\)(N) = (p-1) · (q-1):
\(\phi\)(3337) = (47-1) · (71-1) = 3220
- sceglie e tale che: e < \(\phi\)(N) e MCD(e, \(\phi\)(N)) = 1 (cioè e coprimo con \(\phi\)(N)):
e = 79
- calcola d tale che: e · d ≡ 1 mod((p-1) · (q-1)):
d = 79-1 mod(3220) = 1019
infatti:79 · 1019 = 80501 ≡ 1 mod(3220)
- la chiave pubblica è:
(e, N) = (79, 3337)
- la chiave privata è:
(d, N) = (1019, 3337)
Adesso Alice è libera di pubblicare la sua chiave pubblica su Internet, o su un qualsiasi altro elenco disponibile a chiunque voglia scriverle messaggi cifrati.
Supponiamo allora che Bob le voglia mandare un messaggio costituito da m = 688, e vediamo quale operazioni deve eseguire.
Operazioni effettuate da Bob (Cifratura):
- calcola c = me mod(N):
c = 68879 mod(3337) = 1570
- c rappresenta il messaggio cifrato che può essere letto (decifrato) solo da chi è in possesso della chiave privata e quindi solo da Alice. Bob può quindi spedire in tutta tranquillità *c* senza preoccuparsi del fatto che Eva possa intercettarlo, poiché anche in quell’eventualità non sarebbe in grado di volgerlo in chiaro.
Operazioni effettuate da Alice (Decifratura):
- ricevuto il messaggio Alice ricava m mediante la formula m = cd mod(N):
m = 15701019 mod(3337) = 688
L’unico modo di decifrare il messaggio è di conoscere d e gli unici modi che ha Eva per ottenerlo sono ottenerlo da Alice (che non lo vuole rivelare a nessuno) oppure riuscire a ottenere p e q dalla fattorizzazione di N e quindi riuscire a calcolare d a partire da e come ha fatto Alice. Come detto precedentemente, il processo di fattorizzazione di un numero nei suoi fattori primi è un processo molto lungo, specialmente se si ha a che fare con numeri molto grandi (attualmente le chiavi considerate sicure sono lunghe 2048 bit). La segretezza nella comunicazioni tra Alice e Bob è quindi assicurata!
Doppia cifratura
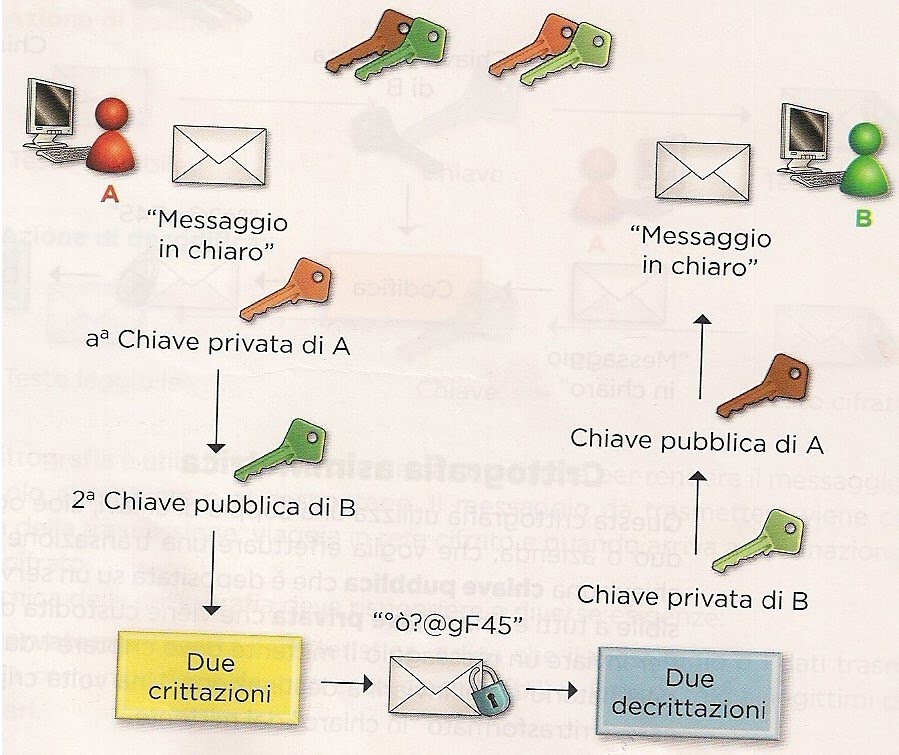
Schema della doppia cifratura in RSA

Dall'immagine si può vedere che Alice non si limita a cifrare il messaggio con la chiave pubblica di Bob ma esegue prima un'altra cifratura con la propria chiave privata; in questo modo Bob, aggiungendo una seconda decifratura con la chiave pubblica di Alice, sarà sicuro che solo Alice può aver cifrato e spedito il messaggio perchè è l'unica persona che conosce la chiave privata di Alice.
Con le operazioni fin qui descritte Alice e Bob sono riusciti ad assicurarsi solo il primo dei quattro obiettivi della crittografia: la riservatezza dei dati, ma non non gli altri tre. Per questo motivo RSA prevede una doppia cifratura.
Dall’immagine si può vedere che Alice non si limita a cifrare il messaggio con la chiave pubblica di Bob ma esegue prima un’altra cifratura con la propria chiave privata; in questo modo Bob, aggiungendo una seconda decifratura con la chiave pubblica di Alice, sarà sicuro che solo Alice può aver cifrato e spedito il messaggio perchè è l’unica persona che conosce la chiave privata di Alice. Il secondo e il quarto obiettivo: autenticazione dell’utente e non ripudio sono quindi stati raggiunti.
Nelle comunicazioni digitali, l’autenticazione degli interlocutori è molto importante e nella maggior parte dei protocolli attualmente utilizzati per le comunicazioni sicure (come TLS) è prevista una fase di autenticazione in cui solitamente viene proprio usato RSA.
Per garantire anche il raggiungimento dell’ultimo obiettivo: l’integrità dei dati, è necessario utilizzare insieme ad RSA altri strumenti, come le funzioni crittografiche di hash, ma questo è vero in generale per tutti i sistemi di comunicazione.
Numeri primi e RSA
Se da un lato la capacità di fattorizzare numeri ci permette di attaccare RSA, la conoscenza di numeri primi molto “grandi” ci permette di effettuare cifrature RSA sempre più potenti. La ricerca di tali numeri costituisce quindi un vero e proprio business, e molte aziende hanno come solo scopo quello di trovarne di sempre più grandi.
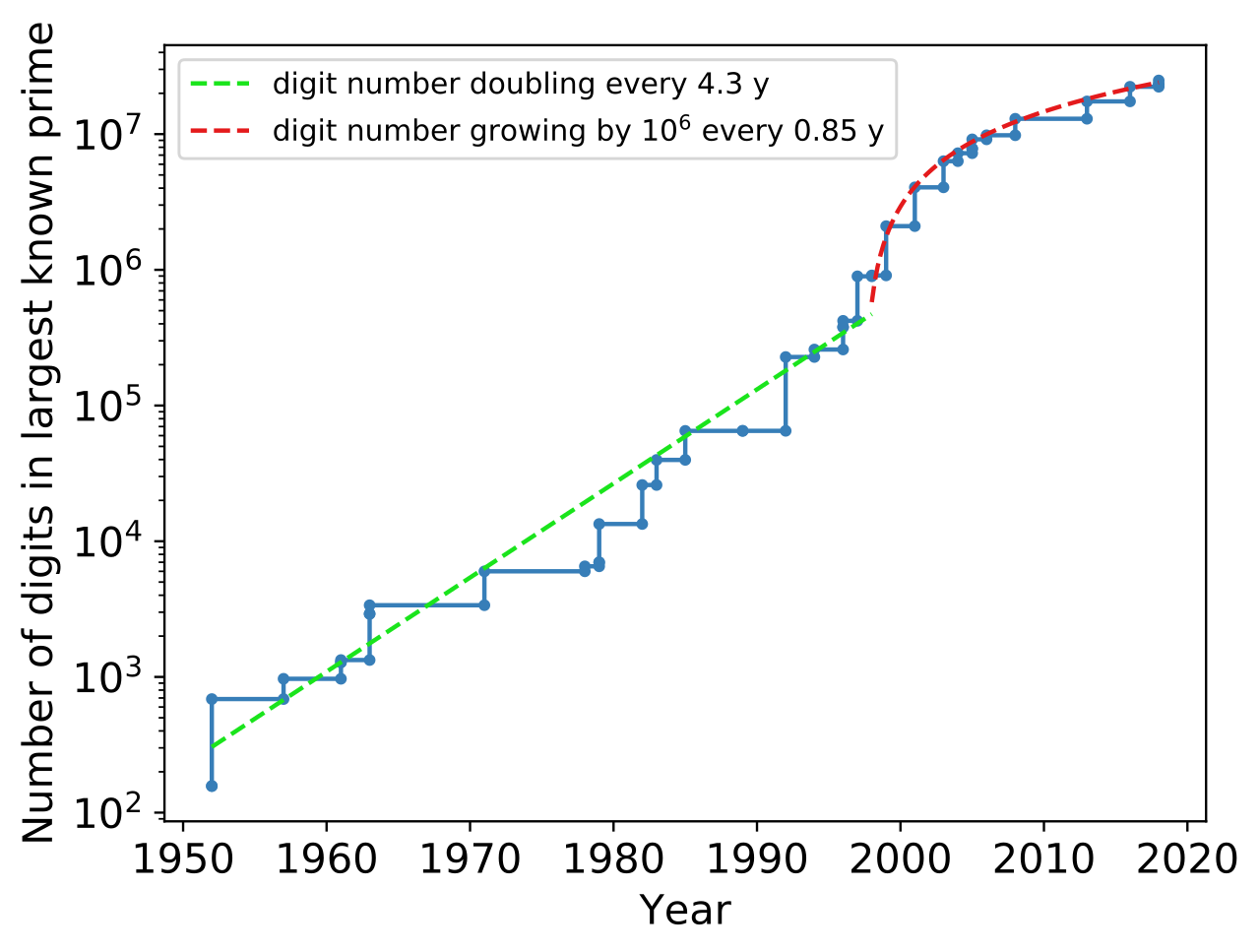
Un grafico aggiornato al 2016 del numero di cifre componenti il più grande numero primo conosciuto. La scala dell'asse delle ordinate è logaritmica. La linea rossa è la curva esponenziale che meglio si adatta al grafico e ha equazione: y = exp(0,187394 t − 360,527), dove t è in anni.

Un grafico aggiornato al 2016 del numero di cifre componenti il più grande numero primo conosciuto. La scala dell'asse delle ordinate è logaritmica. La linea rossa è la curva esponenziale che meglio si adatta al grafico e ha equazione: y = exp(0,187394 t − 360,527), dove t è in anni.
Il più grande numero primo conosciuto è, a ottobre 2020, 282 589 933 − 1, un numero che, se scritto in base 10, è composto da 24 862 048 cifre. Tale numero è stato scoperto il 7 dicembre 2018 da Patrick Laroche nell’ambito del progetto Great Internet Mersenne Prime Search (GIMPS).
I numeri della forma 2n - 1 sono detti numeri di Mersenne e sono indicati con Mn. In generale questi numeri non sono primi, nemmeno se n è primo (per esempio M11 = 2047 = 89 · 23); non si sa nemmeno se di numeri di Mersenne primi ce ne siano un numero finito o se siano infiniti.
Dopo il 1992 tutti i numeri primi più grandi conosciuti sono stati numeri primi di Mersenne, l’ultimo numero primo non di Mersenne ad aver detenuto il suddetto record è stato 391 581 × 2216 193 − 1, scoperto nel 1989.
Attaccare RSA - La fattorizzazione
Abbiamo visto che per attaccare RSA è necessario effettuare la fattorizzazione di N, ma come si fa a fattorizzare un numero così grande? La trattazione approfondita del problema la lasciamo ai matematici ma per capire l’entità del problema facciamo alcuni ragionamenti.
A prima vista, sapendo che si usano numeri primi vicini a 2128, si potrebbe pensare di costruirsi una tabella dei numeri che sono prodotto di due tali primi. Ma quanti sono?
In base al teorema dei numeri primi sappiamo che:
dove \(\pi(n)\) rappresenta il numero di primi minori o uguali a n.
Dunque possiamo rozzamente valutare \({\pi(2^{128})}\) come:
\[{\frac{2^{128}}{log(2^{128})} \approx 3 · 10^{36}}\]e \({\pi(2^{127})}\) come:
\[{\frac{2^{127}}{log(2^{127})} \approx 2 · 10^{36}}\]e quindi \({\pi(2^{128})-\pi(2^{127}) \approx 10^{36}}\). Stiamo cauti nella stima e diciamo che ne abbiamo almeno 1030 (in realtà potremmo anche dire con sicurezza 1035 ). I prodotti di due numeri di questa forma sono allora dell’ordine di 1060. Immagazzinarli in forma binaria richiede allora \({2^{256} \cdot 10^{60} \approx 2^{256} \cdot 2^{199} = 2^{455}}\) bit, quindi \({2^{452} \approx 10^{136} }\) byte. Un terabyte è circa 1012 byte, quindi servirebbe qualcosa come 10124 terabyte. Troppi anche solo da immaginare: il diametro della Galassia in metri è 1021.
Più sensato è pensare di fattorizzare N, ma l’unico modo conosciuto è di dividerlo successivamente per 2, 3, e così via. E’ probabile che, nel momento in cui si è ottenuta la fattorizzazione richiesta, la chiave pubblica sia cambiata da parecchi mesi , si faccia un conto approssimativo del tempo richiesto.
Un numero semiprimo (anche detto biprimo o 2-quasi primo, o pq numero) è un numero naturale che è il prodotto di numeri primi (non necessariamente distinti). I primi numeri semiprimi sono: 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, 33, 34, 35, 38, 39, 46, 49, 51, 55, 57, 58, 62, 65, 69, 74, 77, 82, 85, 86, 87, 91, 93, 94, 95, 106.
La RSA Laboratories fondata dai creatori dell’omonimo sistema di crittografia, ha proposto nel 1991 una sfida, la Factoring Challenge, in cui si offrivano premi in denaro a chi riuscisse a fattorizzare una serie di numeri semiprimi da usare come valori di N (semiprimi perchè prodotto dei due primi p e q). In questa pagina sono riportati i risultati raggiunti finora. Nonostante la gara sia stata dichiarata conclusa nel 2007 la ricerca delle soluzioni è ancora in corso e ad oggi (gennaio 2021) il numero più grande fattorizzato è RSA-250 un numero composto da 250 cifre decimali o 829 bits
RSA-250 =
2140324650240744961264423072839333563008614715144755017797754920881418023447140136643345519095804679610992851872470914587687396261921557363047454770520805119056493106687691590019759405693457452230589325976697471681738069364894699871578494975937497937
RSA-250 =
64135289477071580278790190170577389084825014742943447208116859632024532344630238623598752668347708737661925585694639798853367
×
33372027594978156556226010605355114227940760344767554666784520987023841729210037080257448673296881877565718986258036932062711
In matematica, RSA-2048 è il più grande dei numeri RSA (semiprimi grandi che fanno parte del RSA Factoring Challenge). RSA-2048 è un numero con 617 cifre decimali (2048 bits) e probabilmente la sua fattorizzazione non varrà raggiunta ancora per alcuni decenni.
RSA-2048 =
25195908475657893494027183240048398571429282126204032027777137836043662020707595556264018525880784406918290641249515082189298559149176184502808489120072844992687392807287776735971418347270261896375014971824691165077613379859095700097330459748808428401797429100642458691817195118746121515172654632282216869987549182422433637259085141865462043576798423387184774447920739934236584823824281198163815010674810451660377306056201619676256133844143603833904414952634432190114657544454178424020924616515723350778707749817125772467962926386356373289912154831438167899885040445364023527381951378636564391212010397122822120720357
Per un elenco completo dei numeri RSA puoi guardare qui
Lunghezza della chiave in RSA
Per quanto riguarda le dimensioni delle chiavi da utilizzare, nel 2003 la RSA ha dichiarato che una sua chiave a 1024 bit è equivalente a una chiave simmetrica a 80 bit, una sua chiave a 2048 bit è equivalente a una chiave simmetrica a 112 bit e la chiave a 3072 bit è equivalente a una chiave a 128 bit. RSA raccomanda di utilizzare chiavi ad almeno 1024 bit se si intende mantenere sicuri i documenti fino al 2010 e di utilizzare una chiave a 2048 bit se si vogliono documenti sicuri fino al 2030. La chiave a 3072 è indicata per i documenti che devono rimanere sicuri oltre il 2030. Un documento della NIST definisce una chiave asimmetrica a 15360 bit equivalente a una chiave simmetrica 256 bit.
Quando si sceglie la dimensione della chiave da utilizzare bisogna tenere a mente che per effettuare un qualsiasi attacco è necessario investire una certa quantità di risorse, che si possono tradurre anche in termini economici, e maggiori saranno le risorse investite maggiore sarà la velocità con cui si potrà effettuare l’attacco. Si sarà quindi disposti a fare un attacco solo nel caso le informazioni da scoprire abbiano un valore che valga la spesa richiesta. Ad esempio è interessante notare quanto detto alla conferenza Crypto ‘93 (ormai tantissimi anni fa ma il concetto è valido ancora oggi), da M. Wiener del Bell Northern Research, il quale ha descritto come con un milione di dollari sia realizzabile un chip speciale da 50 milioni di test al secondo che, in parallelo ad altri 57.000, può condurre un attacco con successo mediamente in 3,5 ore. Con un costo di 10 milioni di dollari il tempo si abbassa a 21 minuti, e con 100 milioni a disposizione, il codice è infranto in pochi secondi!
Funzioni crittografiche di Hash

Una funzione crittografica di hash al lavoro (SHA1). Anche piccole modifiche ai dati di ingresso causano un notevole cambiamento dell’uscita: si tratta del cosiddetto effetto valanga.

Una funzione crittografica di hash al lavoro (SHA1). Anche piccole modifiche ai dati di ingresso causano un notevole cambiamento dell’uscita: si tratta del cosiddetto effetto valanga.
Una funzione crittografica di hash, in informatica, è una classe speciale delle funzioni di hash che dispone di alcune proprietà che lo rendono adatto per l’uso nella crittografia.
Si tratta di un algoritmo matematico che mappa dei dati di lunghezza arbitraria (messaggio) in una stringa binaria di dimensione fissa chiamata valore di hash (spesso abbreviato impropriamente per comodità in hash), ma spesso viene indicata anche con altri termini come il termine inglese message digest (o semplicemente digest) oppure, se applicata a un file (o documento), come impronta digitale del file (o documento). Tale funzione di hash è progettata per essere unidirezionale (one-way), ovvero una funzione difficile da invertire: l’unico modo per ricreare i dati di input dall’output di una funzione di hash ideale è quello di tentare una ricerca di forza-bruta di possibili input per vedere se vi è corrispondenza (match). In alternativa, si potrebbe utilizzare una tabella arcobaleno di hash corrispondenti.
La funzione crittografica di hash ideale deve avere alcune proprietà fondamentali:
- deve identificare univocamente il messaggio, non è possibile che due messaggi differenti, pur essendo simili, abbiano lo stesso valore di hash;
- deve essere deterministico, in modo che lo stesso messaggio si traduca sempre nello stesso hash;
- deve essere semplice e veloce calcolare un valore hash da un qualunque tipo di dato;
- deve essere molto difficile o quasi impossibile generare un messaggio dal suo valore hash se non provando tutti i messaggi possibili.
Tali caratteristiche permettono alle funzioni crittografiche di hash di trovare ampio utilizzo in tutti quei contesti in cui sia necessario ottenere un’impronta digitale di un messaggio al fine di poterne poi verificare l’integrità.
Proprietà
In generale una funzione di hash è progettata per prendere in input una stringa di qualsiasi lunghezza e produrre in output un valore di hash di lunghezza fissa. Per poter essere considerata funzione crittografica di hash questa funzione deve essere in grado di resistere a tutti gli attacchi basati sulla crittoanalisi: per fare questo deve rispettare le tre seguenti proprietà:
- Resistenza alla preimmagine:
Dato un valore di hash h, deve essere difficile risalire ad un messaggio m con hash(m) = h. Questa proprietà deriva dal concetto di funzione unidirezionale. Funzioni che non dispongono di questa proprietà sono vulnerabili agli attacchi alla preimmagine.
- Resistenza alla seconda preimmagine:
Dato un input m1, deve essere difficile trovare un secondo input m2 tale che hash(m1) = hash(m2). Funzioni che non dispongono di questa proprietà sono vulnerabili agli attacchi alla seconda preimmagine.
- Resistenza alla collisione:
Dati due messaggi m1 ed m2, deve essere difficile che i due messaggi abbiano lo stesso hash, quindi con hash(m1) = hash(m2). Tale coppia è chiamata collisione di hash crittografica. Questa proprietà a volte è indicata come forte resistenza alla collisione. La resistenza alla collisione implica una resistenza alla seconda preimmagine, ma non implica la resistenza alla preimmagine: rispetto a quest’ultimo, richiede un valore di hash almeno due volte più lungo, altrimenti le collisioni possono essere trovate da un attacco del compleanno.
Queste proprietà implicano che un eventuale attacco non permetta di rimpiazzare o modificare un messaggio senza conseguenze sul risultante valore di hash. Pertanto, se due stringhe hanno lo stesso digest, si può essere fiduciosi nel pensare che siano identiche. In particolare, la resistenza alla seconda preimmagine dovrebbe impedire ad un avversario maligno di elaborare un messaggio con lo stesso hash di un messaggio che l’avversario stesso non può controllare. La resistenza alla collisione, invece, impedisce all’attaccante di creare due messaggi distinti con lo stesso hash.
Applicazioni
Verifica dell’integrità di un messaggio
Un’importante applicazione delle funzioni crittografiche di hash è nella verifica dell’integrità di un messaggio. Per mezzo di tali funzioni è possibile determinare, ad esempio, se sono state compiute modifiche ad un messaggio (o ad un file) confrontando il suo hash prima e dopo la trasmissione. Un particolare uso ne viene fatto nella maggior parte degli algoritmi di firma digitale, i quali utilizzano le funzioni di hash al fine di produrre una firma tale da garantire l’autenticità di un messaggio, evitando che un possibile destinatario modifichi un documento firmato da qualcun altro. Per questo motivo il valore di hash viene anche detto impronta digitale del messaggio. La verifica quindi dell’autenticità del valore di hash del messaggio viene considerata come prova di autenticità del messaggio stesso.
Identificatore di file o dati
In quelle applicazioni in cui si necessita di gestire grandi quantitativi di file, un digest dei messaggi può anche essere utile nell’identificazione di essi in maniera affidabile. Diversi sistemi di gestione di codice sorgente, tra cui Git, Mercurial e Monotone, utilizzano il sha1sum (un algoritmo che calcola e verifica gli hash SHA-1) di vari tipi di contenuti (contenuti di file, alberi di directory, informazioni genealogiche, ecc.) per identificarli in modo univoco. Lo stesso obiettivo vuole essere raggiunto dalle reti di condivisione di file peer-to-peer dove, ad esempio, in un link ed2k, un hash di tipo MD4 è combinato con la dimensione del file, fornendo informazioni sufficienti per individuare le origini del file stesso, scaricarlo e verificarne il contenuto. I collegamenti magnetici (magnet links) ne costituisce un altro esempio. Avendo a disposizione funzioni hash di un certo tipo, una delle principali applicazioni delle funzioni crittografiche è quella di consentire la rapida ricerca di dati in una tabella hash. Tuttavia, rispetto alle funzioni di hash standard, le funzioni crittografiche di hash tendono ad essere più dispendiose in termini di calcolo. Per questo motivo, vengono utilizzate in contesti in cui è necessario che gli utenti siano protetti dalla possibilità di contraffazione (creazione di dati con lo stesso digest) da parte di partecipanti potenzialmente dannosi.
Verifica delle password
Nelle applicazioni che necessitano di un’adeguata autenticazione è troppo rischioso memorizzare le password di tutti gli utenti in chiaro, cioè su un file non cifrato, soprattutto nel caso in cui quest’ultimo venga compromesso. Un modo per evitare di andare incontro a una vera e propria violazione della sicurezza è quello di memorizzare solo il valore di hash di ogni password: una volta avvenuta l’autenticazione da parte dell’utente, viene calcolato l’hash della password da lui inserita e il risultato viene confrontato con l’hash memorizzato in precedenza. Spesso, la password viene concatenata con un valore casuale e non segreto, denominato salt, prima ancora che venga applicata la funzione hash. Utilizzati insieme, ma memorizzati separatamente, producono un output che sostituisce le sole password, consentendo dunque agli utenti di autenticarsi. Tenendo in considerazione il sale e il fatto che, generalmente, gli utenti ne possiedono diversi, non è possibile archiviare tabelle di valori di hash pre-computati per le password comuni. Però, come già accennato in precedenza, essendo da un lato le password dei messaggi brevi e le funzioni di hash progettate per essere calcolate rapidamente dall’altro, è possibile essere soggetti ad attacchi di forza bruta (basta considerare che la GPU può provare miliardi di possibili password al secondo). In compenso, esistono delle funzioni, denominate funzioni di stretching della chiave, come PBKDF2, Bcrypt o Scrypt che “potenziano” le password per renderle più sicure di fronte ad un attacco di forza bruta.
Proof-of-Work
Il sistema Proof-of-work è una misura economica per scoraggiare attacchi di tipo denial of service e altri abusi di servizio (come lo spam su una rete) che impone certi lavori da parte del richiedente del servizio, di solito intesi come tempo di elaborazione di un computer. Una caratteristica fondamentale di questi sistemi è la loro asimmetria: il lavoro deve essere moderatamente complesso (ma fattibile) sul lato richiedente, ma nello stesso tempo, per il fornitore di servizi (service provider) risulta semplice da controllare. Un sistema famoso, usato nella generazione di bitcoin e in Hashcash, usa inversioni di hash parziali per verificare che il lavoro sia stato fatto, in modo tale da sbloccare una ricompensa (detto reward di Bitcoin) nel caso di Bitcoin o come un token di buona volontà da inviare via e-mail ad Hashcash. In pratica, il mittente è tenuto a trovare un messaggio il cui valore hash inizia con un numero di bit zero: il lavoro medio che egli deve eseguire per trovare un messaggio valido è esponenziale nel numero di bit zero richiesti nel valore hash. D’altra parte, il destinatario può verificare la validità del messaggio eseguendo una singola funzione hash. Ad esempio, in Hashcash, se ad un mittente venisse richiesto di generare un header il cui valore hash SHA-1 a 160 bit ha come primi 20 bit degli zeri, dovrà in media provare 219 volte prima di trovare un header valido.
Generazione di numeri pseudocasuali e chiavi di derivazione
Le funzioni di hash possono essere impiegate anche per la generazione di stringhe pseudorandom o per la derivazione di chiavi e password da una singola chiave o password sicura.
Attacchi alle funzioni crittografiche di hash
I possibili attacchi ad una funzione crittografica di hash si possono riassumere in due categorie:
- Attacco alla preimmagine cioè trovare il messaggio da cui è stato calcolato un certo valore di hash.
Di solito si vuole fare questo attacco quando si vuole scoprire una password di cui è stato salvato il valore di hash, argomento di cui si è parlato qui
- Attacco alla seconda preimmagine che consiste nel trovare una collisione ovvero trovare due messaggi che producano lo stesso valore di hash.
Trovare delle collisioni permette ad un attaccante di sostituire un messaggio con un messaggio differente che produce lo stesso valore di hash
Algoritmi di hash crittografico
Al giorno d’oggi esistono molte funzioni crittografiche di hash che vengono usate in molti contesti differenti. Nel tempo alcune di esse sono diventate obsolete perchè non più sicure all’aumentare della potenza di calcolo disponibile.
Di seguito sono riportate le funzioni crittografiche di hash più usate. Una lista più completa può essere consultata qui.
MD5
MD5 was designed by Ronald Rivest in 1991 to replace an earlier hash function, MD4, and was specified in 1992 as RFC 1321. Collisions against MD5 can be calculated within seconds which makes the algorithm unsuitable for most use cases where a cryptographic hash is required. MD5 produces a digest of 128 bits (16 bytes).
SHA-1
SHA-1 was developed as part of the U.S. Government’s Capstone project. The original specification – now commonly called SHA-0 – of the algorithm was published in 1993 under the title Secure Hash Standard, FIPS PUB 180, by U.S. government standards agency NIST (National Institute of Standards and Technology). It was withdrawn by the NSA shortly after publication and was superseded by the revised version, published in 1995 in FIPS PUB 180-1 and commonly designated SHA-1. Collisions against the full SHA-1 algorithm can be produced using the shattered attack and the hash function should be considered broken. SHA-1 produces a hash digest of 160 bits (20 bytes).
Documents may refer to SHA-1 as just “SHA”, even though this may conflict with the other Secure Hash Algorithms such as SHA-0, SHA-2, and SHA-3.
SHA-2
SHA-2 (Secure Hash Algorithm 2) is a set of cryptographic hash functions designed by the United States National Security Agency (NSA), first published in 2001. They are built using the Merkle–Damgård structure, from a one-way compression function itself built using the Davies–Meyer structure from a (classified) specialized block cipher.
SHA-2 basically consists of two hash algorithms: SHA-256 and SHA-512. SHA-224 is a variant of SHA-256 with different starting values and truncated output. SHA-384 and the lesser-known SHA-512/224 and SHA-512/256 are all variants of SHA-512. SHA-512 is more secure than SHA-256 and is commonly faster than SHA-256 on 64-bit machines such as AMD64.
The output size in bits is given by the extension to the “SHA” name, so SHA-224 has an output size of 224 bits (28 bytes); SHA-256, 32 bytes; SHA-384, 48 bytes; and SHA-512, 64 bytes.
| Algoritmo e variante | Dimensione dell’output (bit) | Dimensione dello stato interno (bit) | Dimensione del blocco (bit) | Max. dimensione del messaggio (bit) | Dimensione della word (bit) | Passaggi | Operazioni | Collisioni trovate |
|---|---|---|---|---|---|---|---|---|
| SHA-0 | 160 | 160 | 512 | 264 − 1 | 32 | 80 | +,and,or,xor, rotl | Sì |
| SHA-1 | 160 | 160 | 512 | 264 − 1 | 32 | 80 | +,and,or,xor, rotl | Attacco 263 |
| SHA-2 (SHA-256/224) | 256/224 | 256 | 512 | 264 − 1 | 32 | 64 | +,and,or,xor,shr, rotr | Nessuna |
| SHA-2 (SHA-512/384) | 512/384 | 512 | 1024 | 2128 − 1 | 64 | 80 | +,and,or,xor,shr, rotr | Nessuna |
SHA-3
SHA-3 (Secure Hash Algorithm 3) was released by NIST on August 5, 2015. SHA-3 is a subset of the broader cryptographic primitive family Keccak. The Keccak algorithm is the work of Guido Bertoni, Joan Daemen, Michael Peeters, and Gilles Van Assche. Keccak is based on a sponge construction which can also be used to build other cryptographic primitives such as a stream cipher. SHA-3 provides the same output sizes as SHA-2: 224, 256, 384, and 512 bits.
Configurable output sizes can also be obtained using the SHAKE-128 and SHAKE-256 functions. Here the -128 and -256 extensions to the name imply the security strength of the function rather than the output size in bits.
Firma digitale
La firma è la sottoscrizione del proprio nome, o di uno pseudonimo, per chiudere un’opera d’arte o una scrittura, confermarla o renderne noto l’autore. Per questo motivo caratteristiche fondamentali della firma sono la sua unicità e il suo carattere personale. Il termine deriva dalla parola latina firmus, nel senso di definito, inamovibile.
La definizione appena data definisce il concetto classico di firma. Con l’avvento della digitalizzazione si è presentata la necessità di avere un corrispettivo digitale della normale firma autografa, qualcosa che permetta di dimostrare l’autenticità di un messaggio o di un documento digitale garantendo a chi legge tale documento che:
- sia possibile verificare l’identità di chi ha firmato il documento (autenticazione),
- il messaggio non sia stato modificato dopo l’apposizione della firma (integrità).
- chi firma il documento non possa negare di averlo fatto (non ripudio)
Si può facilmente notare che queste tre condizioni corrispondono ai quattro obiettivi della crittografia tolto quello riguardante la riservatezza, poichè in questo caso il documento non deve essere segreto, ma solo firmato.
Per raggiungere questi obiettivi si ricorre all’utilizzo di due strumenti precedentemente descritti: una funzione crittografica di hash e un algoritmo di crittografia asimmetrica, tipicamente RSA.
L’utilizzo di RSA permette di raggiungere gli obiettivi 1 e 3 poichè il firmatario può generare una coppia di chiavi pubblica privata e:
- cifrare il documento con la propria chiave privata,
- allegare al documento cifrato i propri dati personali,
- depositare la propria chiave pubblica, insieme ai propri dati personali presso un ente certificatore, che nella pratica in Italia possono essere ad esempio le Poste Italiane o la Camera di Commercio e che garantirà la corrispondenza tra i dati personali e la chiave pubblica;
in questo modo chiunque legga il documento può prelevare la chiave pubblica corrispondente ai dati personali allegati alla firma per decifrare il documento ed essere sicuro dell’identità del firmatario.
Con queste sole operazioni non è però garantita l’integrità del documento. Per raggiungere anche questo obiettivo è necessario usare anche una funzione crittografica di hash la cui principale applicazione è proprio quello di ottenere l’impronta diditale di un documento. La sequenza di operazioni da effettuare va quindi modificata come segue:
- calcolare il valore di hash corrispondente al documento;
- cifrare il valore di hash calcolato con la propria chiave privata e non l’intero documento, anche perchè l’obiettivo non è rendere segreto il documento ma solo firmarlo;
- depositare la propria chiave pubblica, insieme ai propri dati personali presso un ente certificatore, che nella pratica in Italia possono essere ad esempio le Poste Italiane o la Camera di Commercio e che garantirà la corrispondenza tra i dati personali e la chiave pubblica (nessuna differenza rispetto a prima);
- allegare al documento il valore di hash cifrato e i propri dati personali
in questo modo chiunque legga il documento può prelevare la chiave pubblica corrispondente ai dati personali allegati alla firma per decifrare il valore di hash e ricalcolare da se il valore di hash del documento e confrontare i due valori (quello decifrato dalla firma e quello ottenuto dal documento in chiaro ricevuto); se i due valori coincidono allora si può essere sicuri che documento e firma siano integri e autentici. I tre obiettivi sono stati raggiunti.
Contraffare una firma digitale
Ceracare di contraffare una firma o un documento firmato, equivale ad effettuare un attacco a uno o entrambi i sistemi crittografici usati.
Se si vuole modificare il documento senza modificare la firma è necessario trovare una collisione della funzione crittografica di hash ovvero trovare un documento che produca lo stesso hash del documento originale.
Se si vuole firmare un documento con la firma di un’altra persona è necessario attaccare RSA e scoprire la chiave segreta di quella persona.
Entrambi questi scenari sono stati ampiamente trattati nelle sezioni riguardanti gli attacchi alle funzioni crittografiche di hash e a RSA.
Come usare nella pratica la firma digitale
Nella pratica per poter utilizzare la firma digitale devo per prima cosa contattare un ente certificatore. In Italia gli enti certificatori, per poter rilasciare firme digitali, devono essere autorizzati da AgID, l’ente nazionale per la digitalizzazione della Pubblica Amministrazione. è possibile reperire qui una lista completa dei prestatori di servizi fiduciari attivi in Italia compresa di link alla pagina di aquisto del servizio che ha un costo che si aggira sui 50€ all’anno.
Una volta acquistato il servizio, l’ente certificatore si occupa di verificare l’identità di chi ha richiesto il servizio e rilascia uno o più dispositivi accompagnati da un software necessari all’applicazione delle firme ai documenti. I dispositivi possono essere una smart card (che contiene una sim) accompagnata da lettore oppure un’apposita chiavetta usb chiamata token usb provvista di sim.
Il software fornito per la firma dei documenti normalmente è in grado di firmare documenti pdf producendo un nuovo file in formato p7m che conterrà sia documento in chiaro che firma. Solitamente è possibile firmare documenti anche di formati differenti anche se il formato pdf è quello più supportato. Nel momento dell’apposizione della firma il software richiederà di poter comunicare con la sim, ricevuta tramite chiavetta o lettore di smart card, dove risiede la chiave privata necessaria per la firma. Per sicurezza l’accesso alla sim è protetto con un pin.
Di seguito è proposto il video informativo creato dalla camera di commercio di Milano, Monza Brianza, Lodi su che cos’è e come ottenere la firma digitale.
Riferimenti esterni
- Crittografia simmetrica su Wikipedia.
- Crittografia asimmetrica su Wikipedia.
- Piccolo teorema di Fermat su Wikipedia.
- Teorema cinese del resto su Wikipedia.
- Crittografia da Atbash a RSA di Paolo Bonavoglia.
- Teorema dei numeri primi su Wikipedia.
- Numeri RSA su Wikipedia.
- DES su Wikipedia