Teoria della Complessità Computazionale
Indice
- I problemi e la loro complessità
- Analisi della complessità degli algoritmi
- La complessità dei problemi
- Riferimenti esterni
- Altro materiale da guardare
I problemi e la loro complessità
La teoria della complessità computazionale si pone come obiettivo quello di analizzare la complessità dei problemi in modo da poterli catalogare e confrontare in base alla loro difficoltà. In questo capitolo verranno trattate le modalità con cui è possibile valutare la complessità dei problemi. Per poterlo fare è necessario iniziare a definire alcuni concetti fondamentali.
Problema e Algoritmo risolutivo
In informatica, così come in matematica, un problema è una relazione tra un insieme di istanze e un insieme di soluzioni. La descrizione del problema può essere data in molte forme, con un linguaggio naturale o con un linguaggio matematico, e pone sempre un quesito per cui date una serie di premesse si chiede di trovare una o più soluzioni che soddisfino determinate condizioni. La descrizione del problema spesso prevede che in input venga fornita una serie di valori o variabili che aquistano un valore diverso per ogni istanza del problema
Il concetto di istanza, che dovrebbe essere familiare ad un informatico, si può definire in questo contesto come una specifica formulazione del problema per cui sono stati assegnati determinati valori alle variabili in input.
Esempio
Problema 1: determinare se un numero è primo.
Ogni numero che può essere fornito in input al problema rappresenta un istanza del problema, cioè:
I1 = 3, I2 = 6, I3 = 7, …, In = 127 …
Problema 2: Ordinamento di un vettore di n elementi.
Ogni istanza è rappresentata da un diverso vettore vettore da ordinare, vettore che può variare per cardinalità e valori che contiene:
I1 = [5, 7, 2, 1], I2 = [1], I3 = [1, 2, 3, 4], …, In = [4, 77, 128, … 923] …
Il problema numero 2 presenta una caratteristica molto importante per la descrizione di molti problemi: il valore n che indica la dimensione del vettore di input. In generale questo valore definisce la cardinalità dei dati in ingresso o cardinalità dell’input. è evidente che il tempo di esecuzione di un algoritmo può variare anche molto da istanza a istanza e in particolare può cambiare moltissimo al variare del valore di n.
Per poter fornire una soluzione ad ogni istanza del problema è necessario eseguire un algoritmo risolutivo del problema. Se indichiamo con A l’algoritmo, con π il problema e con I l’istanza, possiamo dire che:
A risolve π se applicato ad ogni sua istanza I ne produce la soluzione corretta
Analisi della complessità degli algoritmi
Dalle definizioni date finora risulta evidente la correlazione tra problema e algoritmo risolutivo. Per poter analizzare la complessità dei problemi è quindi necessario passare dall’analisi della complessità degli algoritmi risolutivi del problema. Per poterlo fare è necessario adottare dei criteri con cui valutare la complessità.
Parametri di complessità
I criteri che si possono adottare per valutare la complessità possono essere moltissimi ed è necessario stabilire quali siano quelli più rilevanti e utili nel nostro contesto di lavoro. Alcuni criteri utili in determinati contesti possono essere:
- la semplicità di comprensione o modificabilità del codice sorgente
- l’accessibilità o usabilità dell’interfaccia utente
- la bellezza grafica dell’interfaccia
- …
Questi criteri seppur importanti in certi contesti non sono adatti per valutare la complessità di un algoritmo poichè sono tutti criteri soggettivi e non sono quindi universalmente quantificabili. Questi criteri poi in realtà non ci dicono nulla sull’efficienza dell’algoritmo e quindi sulla complessità del problema risolto.
È quindi necessario identificare criteri di efficienza oggettivi degli algoritmi. Questi criteri sono:
- la complessità temporale che consiste nel tempo impiegato per eseguire l’algoritmo
- la complessità spaziale che indica quanta memoria richiede l’algoritmo per la sua esecuzione
- la complessità di I/O che indica il tempo necessario alle operazioni di imput e output effettuate dall’algoritmo
- la complessità di trasmissione che indica il tempo necessario alla trasmissione o ricezione di dati da componenti remote o altri calcolatori
I due criteri più rilevanti sono i primi due e sono quelli su cui si basa la catalogazione dei problemi, in particolar modo il primo.
La complessità di tempo
Abbiamo definito la complessità di tempo come la quantità di tempo necessaria all’esecuzione dell’algoritmo, questa definizione però è decisamente semplicistica e in realtà inadatta a valutare oggettivamente un algoritmo e quindi un problema. Il motivo di quest’affermazione è che il tempo necessario all’esecuzione di un algoritmo è strettamente dipendente dalle caratteristiche della macchina che esegue l’algoritmo, caratteristiche completamente indipendenti dall’algoritmo stesso il quale può essere eseguito da chiunque. Quello che ci interessa sapere sono le caratteristiche dell’algoritmo indipendentemente da chi lo esegue.
Nella seguente tabella sono indicati in secondi i tempi di esecuzione di due algoritmi A₁ e A₂ che risolvono lo stesso problema su due computer diversi e con differenti dimensioni dell’input.
| Computer 1 | Computer 2 | |||
|---|---|---|---|---|
| n | A₁ | A₂ | A₁ | A₂ |
| 50 | 0,005 | 0,07 | 0,05 | 0,25 |
| 100 | 0,003 | 0,13 | 0,18 | 0,55 |
| 200 | 0,13 | 0,27 | 0,73 | 1,18 |
| 300 | 0,32 | 0,42 | 1,65 | 1,85 |
| 400 | 0,55 | 0,57 | 2,93 | 2,67 |
| 500 | 0,67 | 0,72 | 4,60 | 3,28 |
| 1000 | 3,57 | 1,60 | 18,32 | 7,03 |
Pssiamo osservare che la misurazione in secondi del tempo di esecuzione non è in grado di descrivere la bontà dell’algoritmo perchè dipende sia dalla potenza di calcolo dei computer sia dalla dimensione dell’input.
Nella realtà ci sono anche altri fattori che determinano la velocità di esecuzione dell’algoritmo. Un programmatore sa infatti che i programmi vengono scritti quasi sempre in un linguaggio di programmazione che poi deve essere tradotto nel linguaggio della macchina che lo esegue. Diversi compilatori possono produrre un codice macchina differente più o meno efficiente, inoltre le singole operazioni in linguaggio macchina richiedono tempi di esecuzione differenti, tempi che possono variare anche al variare della CPU.
È necessario quindi trovare una modalità differente per rappresentare la complessità temporale che dipenda esclusivamente dalle caratteristiche dell’algoritmo.
Il primo passaggio da effettuare è introdurre una nuova notazione che permetta di indicare la complessità temporale indipendentemente dalla dimensione dell’input o meglio che mantenga la cardinalità dell’input come generico parametro. Indicheremo quindi il tempo di calcolo con la funzione T(n) che per ora indica un generico tempo di esecuzione in funzione della dimensione dell’input n.
Il secondo passaggio è quello di cambiare completamente l’unità di misura utilizzata per misurare il tempo di calcolo, poichè abbiamo visto che la misurazione in secondi è praticamente inutile. La nuova unità di misura dovrà tener conto solo del numero di operazioni effettuate, a prescindere dallo specifico tempo di esecuzione di tale operazione in un determinato calcolatore.
Dovremo assumere che:
- le seguenti istruzioni elementari abbiano lo stesso tempo di calcolo:
- assegnamento,
- operazioni di I/O,
- operazioni aritmetiche,
- valutazione di espressioni booleane
- qualsiasi accesso alla memoria abbia un costo fisso
- non vi sia alcun grado di parallelismo
- le operazioni abbiano un costo sempre uguale a prescindere dal valore delle variabili coinvolte
In questo modo ogni operazione verrà trattata in egual modo e considerata un’istruzione a costo unitario o passo base. È evidente che questo rappresenta una semplificazione della realtà ma ci permette di svincolare ogni misurazione dalle caratteristiche tecnologiche dei calcolatori e dei compilatori usati.
La funzione T(n) può quindi essere definita nel seguente modo:
La funzione T(n) esprime il numero di passi base necessari affinchè l’algoritmo A possa produrre la soluzione di un’istanza di dimensione n.
Esempi di calcolo della complessità di un algoritmo
Esempio 1
Consideriamo un algoritmo che stampa i primi n numeri interi:
i = 1; // 1 passo base
while (i <= n) // n + 1 passi base
printf("%d ", i) // 1 * n passi base
i = i + 1; // 1 * n passi base
Totale passi base = $ 1 + n + 1 + 2·n = 2 + 2·n $
Esempio 2
Consideriamo un algoritmo che stampa i numeri interi multipli di 2 e 3 minori di n:
for (i = 1; i <= n; i++) // 1 pb per l'inizializzazione
// n+1 pb per il test
// n pb per l'incremento
if (i % 2 == 0 && i % 3 == 0) // 2 * n pb
printf("%d ", i); // 1 * n / x pb
Quando un’istruzione si trova all’interno di un if può essere complicato dire quante volte essa venga eseguita. Come vedremo più avanti bisogna considerare il caso peggiore cioè che l’istanza che stiamo valutando ci costringa ad entrare nell’if il massimo numero di volte possibile. In questo semplice caso possiamo facilmente calcolare che x vale 6. Vedremo poi che la presenza di un coefficiente come 1/6 è del tutto irrilevante nel calcolo della complessità, sarebbe diverso se dovessi moltiplicare o dividere per una funzione di n.
Totale passi base =
\[1+n+1+n + (2 + 1/6)·n =\] \[= 2 + (1 + 1 + 2 + 1/6)·n =\] \[= 2 + 25/6·n\]Esempio 3
Consideriamo un algoritmo che stampa tutti gli elementi di una matrice n·m:
for (i = 0; i < n; i++) // 2 + 2 * n pb
for (j = 1; j < m; j++) // (2 + 2 * m) * n pb
printf("%d ", matrice[i][j]); // 1 * n * m pb
Totale passi base =
\[2+2·n + (2+2·m)·n + n·m =\] \[2 + 2·n + 2·n + 2·n·m + n·m =\] \[2 + 4·n + 3·n·m\]Nel valutare la complessità solitamente non è rilevante la distinzione tra n e m, in particolare se non sappiamo nulla a priori dei valori di n e m. Possiamo quindi valutare la complessità come:
\[2 + 4·n + 3·n^2\]Esempio 4
Consideriamo l’algoritmo bubble sort:
void bubblesort(int a[], int n){
int i, j;
// N.B. n-1 è l'ultima componente dell'array.
for(i = 0; i < n - 1; i++) //scansiona tutto l'array tranne l'ultima componente: n - 1 escluso. Quindi fino al penultimo elemento.
for (j = n - 1; j > i; j--) //j settato all'ultima componente e decresce ad ogni iterazione. Esce dal ciclo solo se j <= i
if (a[j] < a[j-1]) //se la componente corrente è più piccola della precedente, li scambia.
scambia(&a[j],&a[j-1]);
}
//la funzione scambia è così composta:
void scambia(int *a, int *b){ //richiede due indirizzi di memoria in entrata che verranno memorizzati in 2 puntatori.
int temp; //la variabile d'appoggio che memorizza temporaneamente il valore di a.
temp = *a;
*a = *b;
*b = temp;
}
Questo algoritmo è decisiamente più complesso dei precedenti e introduce anche la chiamata a funzione. Anche il tempo di chiamata a funzione viene semplificato, come tutte le altre operazioni, e si considerano semplicemente i passi base necessari ai passaggi di valore dei parametri della funzione.
Riprendiamo il codice ripulito da commenti di spiegazione e inseriamo il costo di ogni riga di codice:
void bubblesort(int a[], int n){ // 2
int i, j; // 2
for(i = 0; i < n - 1; i++) // 1 + n + n - 1 = 2 * n
for (j = n - 1; j > i; j--) // (1 + n-i + n-i-1) * (n-1) = 2*(n-i)*(n-1) (variabile in funzione di i !!!)
// mediamente n-i vale n/2
if (a[j] < a[j-1]) // (n-i)*(n-1)
scambia(&a[j],&a[j-1]); // (n-i)*(n-1) nel caso peggiore
}
//la funzione scambia è così composta:
void scambia(int *a, int *b){ // 2
int temp; // 1
temp = *a; // 1
*a = *b; // 1
*b = temp; // 1
}
Quello che notiamo subito è che già con un algoritmo non troppo complesso come il bubble sort, questo metodo di contare ogni singola operazione per valutare la complessità è troppo complicato. È necessario quindi introdurre un metodo più comodo. Nel prossimo capitolo vedremo come lo studio della complessità asintotica può semplificare di molto il calcolo della complessità.
Complessità asintotica
Una volta che è stata definita correttamente la complessità di tempo in termini di numero passi base in funzione della dimensione dell’input è possibile porsi l’obiettivo di confrontare gli algoritmi tra di loro.
Immaginiamo di aver trovato una serie di algoritmi con diversi tempi di calcolo e volerli confrontare tra loro. Supponendo che un passo base richieda 1 microsecondo (10-6 s) per essere eseguito è possibile costruire la seguente tabella che rappresenta i tempi di esecuzione in secondi dei diversi algoritmi al crescere della dimensione dell’input
| n = 10 | n=100 | n=1000 | n=106 | |
| log(n) | 10-6 | 2·10-6 | 3·10-6 | 6·10-6 |
| √n | 3·10-6 | 10-5 | 3·10-5 | 10-3 |
| n+5 | 15·10-6 | 10-4 | 10-3 | 1 s |
| 2·n | 2·10-5 | 2·10-4 | 2·10-3 | 2 s |
| n·log(n) | 10-5 | 2·10-4 | 3·10-3 | 6 s |
| n2 | 10-4 | 10-2 | 1 s | 106 (~12 gg) |
| n2+n | 1,1·10-4 | 1,01·10-2 | 1 s | 106 (~12 gg) |
| n3 | 10-3 | 1 s | 103 (~1 g) | 1012 (~30 secoli) |
| 2n | 10-3 | 1014 secoli | 10285 secoli | —- |
Guardando i risultati si possono subito fare due importanti considerazioni:
- per valori di n piccoli tutti gli algoritmi hanno tempi di calcolo accettabili
- per valori di n grandi gli algoritmi differiscono enormemente
Capiamo subito quindi che per vautare la velocità o meglio la complessità di un algoritmo è necessario studiare il suo comportamento per valori di n grandi cioè, detto in termini matematici, studiare l’andamento asintotico di T(n).
Concentrandoci quindi sugli andamenti asintotici possiamo osservare che gli algoritmi si possono dividere in gruppi che hanno un andamento simile:
- il primo, che ha un andamento logaritmico, mantiene sempre valori di T(n) estremamente bassi rimanendo sempre allo stesso ordine di grandezza
- il secondo, che è un polinomio con grado inferiore a 1, cresce molto lentamente mantenendosi su frazioni di secondo anche con n grandi
- terzo e quarto, che hanno andamento lineare, crescono lentamente mantenendo sempre buoni tempi di calcolo; la presenza di un coefficiente (2) non modifica significativamente la situazione
- il quinto, che combina un andamento lineare con uno logaritmico, non si discosta dai tempi lineari
- gli altri algoritmi con andamento polinomiale con grado superiore a 1, presentano tempi di calcolo accettabili finchè la dimensione dell’input non è troppo grande, poi i tempi diventano inaccettabili
- l’ultimo, che ha un andamento esponenziale, all’aumentare di n raggiunge molto in fretta tempi di calcolo inaccettabili
Queste osservazioni ci permettono di raggruppare in categorie di tempi di calcolo e quindi categorie di complessità temporale i vari algoritmi sulla base dell’andamento asintotico dei tempi di calcolo. Le categorie sono:
- costante (tempo che non dipende da n ma è fisso)
- logaritmico
- polinomiale con grado inferiore a 1
- lineare (polinomiale con grado uguale a 1)
- pseudolineare (n·log(n))
- polinomiale (con grado maggiore di 1)
- esponenziale
- fattoriale
- nn
Nella lista sono state aggiunte per completezza alcune classi non presenti nell’esempio precedente.
Notazioni di complessità asintotica
Per chi conosce la matematica il concetto di andamento asintotico dovrebbe essere chiaro ma è compunque importante trattare questo concetto in maggior dettaglio poichè nella teoria della complessità computazionale sono utilizzate diverse notazioni per esprimere la complessità degli algoritmi (e quindi dei problemi). Notare che quando si parla di complessità solitamente se non si specifica nient’altro si dà per scontato che si sta parlando di complessità temporale ma le notazioni di seguito descritte sono valide anche per le complessità spaziale, di IO e di trasmissione.
O-grande
La funzione O-grande (leggi o grande) è utilizzata per indicare un limite asintotico superiore della nostra funzione T(n) infatti è definita in questo modo:
\[f(n) \in O(g(n)) \text{ per } n \to \infty\]se e solo se
\[\exists n_0 \in \Bbb{R}, \; c > 0 \quad : \quad f(n) ≤ c · g(n) \ ∀ n > n_0\]Prendiamo ad esempio due funzioni:
- $f(n) = 6n^4-2n^3+5$
- $g(n) = n^4$
possiamo dire che $ f(n) \in O(g(n)) $ per $ n \to \infty $, infatti le due funzioni hanno lo stesso grado e $ f(n) $ ha solamente un coefficiente (6) che la rende superiore a $g(n)$ ma la definizione ci consente di scegliere un opportuno coefficiente $c$ per cui moltiplicare $g(n)$ che permette a $g(n)$ di essere superiore a $f(n)$ da un certo valore di n in poi.
In pratica stiamo dicendo che la funzione $f(n)$ ha un andamento asintotico limitato superiormente dalla funzione $g(n)$, senza considerare i coefficienti che come abbiamo visto analizzando questa tabella non sono rilevanti nel considerare gli andamenti asintotici. In altre parole $f(n)$ cresce al massimo come $g(n)$.
È necessario fare una precisazione sulla notazione O-grande: è vero che $f(n) \in O(g(n))$ ma è anche vero che $f(n) \in O(n^5)$ e che $f(n) \in O(2^n)$ poichè entrambe queste relazioni soddisfano la definizione di O-grande e sia $n^5$ che $2^n$ rappresentano un limite oltre il quale $f(n)$ non potrà mai andare asintoticamente. Nonostante sia possibile quindi individuare infinite funzioni superiori a $f(n)$ ha senso individuare solo la funzione più piccola e semplice che indichi il limite superiore di crescita asintotica di $f(n)$.
| $T(n)$ | O-grande | andamento |
|---|---|---|
| $34$ | $O(1)$ | costante |
| $7+3log(n)$ | $O(log(n))$ | logaritmico |
| $7n+12$ | $O(n)$ | lineare |
| $2n+5 log(n)$ | $O(n)$ | lineare |
| $2n · 5log(n)$ | $O(n · log(n))$ | pseudolineare |
| $3n^2+5n$ | $O(n^2)$ | quadratico |
| $2n+5 n·m$ | $O(n^2)$ | quadratico |
| $3^n+5n^3$ | $O(3^n)$ | esponenziale |
| $3^n+5n^3 + n!$ | $O(n!)$ | fattoriale |
Conoscendo la matematica si può arrivare a conclusioni piuttosto semplici ma importanti che nel loro insieme possono essere chiamate algebra degli O-grandi:
- $f(n) \in O(h(n))$ e $g(n) \in O(h(n)) \Rightarrow f(n) + g(n) \in O(h(n))$
- $f(n) \in O(h(n))$ e $g(n) \in O(i(n)) \Rightarrow f(n) · g(n) \in O(h(n) · i(n))$
- $an^k \in O(n^k)$
- $n^k \in O(n^k+i)$ per ogni $i$ positivo
- $f(n) \in O(g(n))$ e $g(n) \in O(h(n)) \Rightarrow f(n) \in O(h(n))$ (proprietà transitiva)
Nel calcolare la complessità di blocchi di codice si possono invece fare le seguenti osservazioni:
- Teorema della somma: la complessità di un blocco costituito da più blocchi in sequenza è quella del blocco di complessità maggiore,
- Teorema del prodotto: la complessità di un blocco costituito da più blocchi annidati è data dal prodotto delle complessità dei blocchi componenti.
Con questi strumenti è possibile calcolare la complessità di qualsiasi algoritmo.
Nonostante la notazione O-grande sia quella più comunemente usata non è nè l’unica nè la più precisa, ne esistono infatti altre due molto importanti.
Ω-grande
La funzione Ω-grande (leggi omega grande) è una funzione piuttosto simile alla funzione O-grande ma è utilizzata per indicare un limite asintotico inferiore della nostra funzione T(n) infatti è definita in questo modo:
\[f(x) \in Ω(g(n)) \text{ per } n \to \infty\]se e solo se
\[\exists x_0 \in \Bbb{R}, \; c > 0 \quad : \quad f(n) ≥ c·g(x) \ ∀ x > x_0\]Prendiamo anche in questo caso le due funzioni:
- $f(n) = 6n^4-2n^3+5$
- $g(n) = n^4$
possiamo dire che $ f(n) \in Ω(g(n)) $ per $ x \to \infty $, infatti le due funzioni hanno lo stesso grado e $ f(n) $ e secondo la definizione possiamo scegliere un opportuno coefficiente $c$ per cui moltiplicare $g(n)$ che permette a $g(n)$ di essere inferiore a $f(n)$ da un certo valore di n in poi.
In pratica stiamo dicendo che la funzione $f(n)$ ha un andamento asintotico limitato inferiormente dalla funzione $g(n)$, senza considerare i coefficienti che sono irrilevanti. In altre parole $f(n)$ cresce almeno come $g(n)$.
Anche in questo caso è necessario fare una precisazione: è vero che $f(n) \in O(g(n))$ ma è anche vero che $f(n) \in O(n^3)$ e che $f(n) \in O(log(n))$ poichè entrambe queste relazioni soddisfano la definizione di Ω-grande e sia $n^3$ che $log(n)$ sono sicuramente inferiori a $f(n)$ per $ x \to \infty $. Nonostante sia possibile quindi individuare infinite funzioni inferiori a $f(n)$ ha senso individuare solo la funzione più grande e semplice che indichi il limite minimo di crescita asintotica di $f(n)$.
Θ-grande
La notazione Θ-grande (leggi teta grande) è una funzione che permette di unire in un’unica notazione le caratteristiche delle due funzioni precedenti, essa indica infatti in modo preciso l’andamento asintotico della funzione T(n). Θ-grande è definita come:
\[f(x) \in Θ(g(n)) \text{ per } n \to \infty\]se e solo se
\[\exists x_0 \in \Bbb{R}, \; c_1 > 0, c_2 > 0 \quad : \quad c_1·g(x) ≤ f(n) ≤ c_2·g(x) \ ∀ x > x_0\]Prendiamo anche in questo caso le due funzioni:
- $f(n) = 6n^4-2n^3+5$
- $g(n) = n^4$
possiamo dire che $ f(n) \in Θ(g(n)) $ per $ x \to \infty $, infatti le due funzioni hanno lo stesso grado e $ f(n) $ e secondo la definizione possiamo scegliere due opportuni coefficienti $c_1$ e $c_2$ per cui moltiplicare $g(n)$ e ottenere due valori uno inferiore e uno superiore a $f(n)$ da un certo valore di n in poi.
In pratica stiamo dicendo che la funzione $f(n)$ ha un andamento asintotico uguale a quello della funzione $g(n)$, senza considerare i coefficienti che sono irrilevanti. In altre parole $f(n)$ cresce asintoticamente come $g(n)$, nè più nè meno.
Confronto tra algoritmi
Una volta calcolate le complessità degli algoritmi espresse con le notazioni O-grande o Θ-grande è immediato effettuare un confronto tra due algoritmi, basta conoscere l’ordine degli infiniti studiati in matematica.
Per il calcolo della complessità c’è però un problema che non è ancora stato preso in considerazione. Per capire di che problema si tratta consideriamo un esempio reale: un algoritmo di ordinamento di un vettore. A prescindere dal tipo di algoritmo è evidente che il tempo di calcolo non dipenderà solo dalla dimensione del vettore (la dimensione n dell’input) ma anche dalla situazione iniziale del vettore. L’ordinamento di un vettore già ordinato richiederà un tempo molto breve, mentre l’ordinamento di un vettore completamente disordinato richiederà molto più tempo. Ci rendiamo facilmente conto che possiamo distinguere tre diverse situazioni che corrispondono a tre complessità potenzialmente molto diverse tra loro:
- caso migliore: è il caso o insieme di casi col minor tempo di calcolo (a parità di n), in questo caso un vettore già ordinato
- caso peggiore: è il caso o insieme di casi col maggior tempo di calcolo (a parità di n)
- caso medio: ipotetico vettore il cui tempo di calcolo è il tempo medio di calcolo di tutte le istanze del problema
Quando si considera la complessità computazionale si fa riferimento al caso peggiore e se non viene specificato nulla si dà per scontato che ci si sta riferendo a quello. Solitamente invece il caso migliore è considerato poco rilevante nel valutare la complessità dell’algoritmo, infatti mentre il caso migliore è solo un caso particolare e fortunato con un tempo di calcolo particolarmente basso il caso peggiore è quello che ci indica effettivamente la capacità dell’algoritmo di trovare la soluzione corretta in qualsiasi situazione.
Per caso medio, a differenza degli altri due, non ci si riferisce ad un caso o ad un insieme di casi reali ma si indende un ipotetico caso il cui tempo di calcolo è il tempo medio di calcolo su tutte le possibili istanze del problema. Non è detto che sia possibile calcolare a priori il tempo medio di calcolo, spesso infatti è necessario calcolare effettivamente il tempo medio per l’esecuzione dell’algoritmo su tante istanze casuali diverse. Il valore ottenuto è un valore molto utile da conoscere perchè indica mediamente in quanto tempo è possibile trovare la soluzione del problema.
Non è detto che in applicazioni reali venga scelto di utilizzare l’algoritmo che abbia la complessità minore che è vautata nel caso peggiore. Un esempio noto è il quick sort, il più usato algoritmo di ordinamento di vettori che ha complessità $Θ(n^2)$ nel caso peggiore e $Θ(n·log(n))$ nel caso medio. Quick sort infatti è preferibile ad altri algoritmi come merge sort che hanno complessità $Θ(n·log(n))$ anche nel caso peggiore e questo a causa di una serie di altri fattori come la complessità spaziale o altri dettagli legati a dettagli implementativi.
Può essere molto interessante approfondire lo studio delle complessità degli algoritmi di ordinamento a partire da qui.
Esempi di calcolo della complessità di un algoritmo con le notazioni di complessità asintotica
Riprendiamo gli esempi visti prima di introdurre le notazioni di complessità asintotica. Vedremo che sfruttando il nuovo metodo il calcolo della complessità risulta molto più semplice e in molti casi (con algoritmi polinomiali senza logaritmi o radici) praticamente immediato.
Esempio 1
Consideriamo un algoritmo che stampa i primi n numeri interi:
i = 1; // 1 passo base
while (i <= n) // n + 1 passi base
printf("%d ", i) // 1 * n passi base
i = i + 1; // 1 * n passi base
Possiamo direttamente tralasciare coefficienti e termini noti e dire immediatamente che la complessità totale dell’algoritmo è data dalla presenza di un ciclo che comporta l’esecuzione di alcuni passi base per n volte. La complessità è quindi:
\[T(n) = O(n)\]Esempio 2
Consideriamo un algoritmo che stampa i numeri interi multipli di 2 e 3 minori di n:
for (i = 1; i <= n; i++) // 1 pb per l'inizializzazione
// n+1 pb per il test
// n pb per l'incremento
if (i % 2 == 0 && i % 3 == 0) // 2 * n pb
printf("%d ", i); // 1 * n / x pb
Anche in questo caso non ci interessano i coefficienti e i termini noti e siccome la presenza dell’“if” comporta solo l’aggiunta di un coefficiente che possiamo trascurare, anche in questo caso il calcolo della complessità è pressochè immediato. La complessità è:
\[T(n) = O(n)\]Esempio 3
Consideriamo un algoritmo che stampa tutti gli elementi di una matrice n·m:
for (i = 0; i < n; i++) // 2 + 2 * n pb
for (j = 1; j < m; j++) // (2 + 2 * m) * n pb
printf("%d ", matrice[i][j]); // 1 * n * m pb
Il calcolo della complessità è anche in questo caso molto semplice. Siccome abbiamo due cicli innestati, possiamo sfruttare il teorema del prodotto che ci dice che la complessità di due blocchi di codice innestati è data dal prodotto delle complessità. La complessità è quindi:
\[T(n) = O(n^2)\]Esempio 4
Consideriamo l’algoritmo bubble sort:
void bubblesort(int a[], int n){ // 2
int i, j; // 2
for(i = 0; i < n - 1; i++) // 1 + n + n - 1 = 2 * n
for (j = n - 1; j > i; j--) // (1 + n-i + n-i-1) * (n-1) = 2*(n-i)*(n-1) (variabile in funzione di i !!!)
// mediamente n-i vale n/2
if (a[j] < a[j-1]) // (n-i)*(n-1)
scambia(&a[j],&a[j-1]); // (n-i)*(n-1) nel caso peggiore
}
//la funzione scambia è così composta:
void scambia(int *a, int *b){ // 2
int temp; // 1
temp = *a; // 1
*a = *b; // 1
*b = temp; // 1
}
Senza introdurre le notazioni di complessità asintotica il calcolo della complessità di questo algoritmo era molto complesso, ma ora la cosa risulta relativamente semplice. Abbiamo un blocco di codice, la funzione bubble sort, che contiene due cicli innestati, il primo di complessità n il secondo di complessità n, a meno di un coefficiente, 1/2, poichè il ciclo su j avviene ogni volta un numero diverso di volte che è mediamente 1/2·(n-1), questo coefficiente è però trascurabile. La complessità dei due cicli insieme è quindi $O(n^2)$.
Bisogna poi considerare che la funzione “scambia” richiede un certo tempo di calcolo che è un tempo $O(1)$. Siccome questo blocco di codice è innestato nei due cicli precedentemente descritti, bisogna calcolare $O(n^2) · O(1) = O(n^2)$.
La complessità totale è quindi:
\[T(n) = O(n^2)\]Esempio 5
Consideriamo l’algoritmo di ricerca dicotomica, un algoritmo che cerca la posizione di un numero in un vettore ordinato di numeri. Chiaramente la ricerca può riguardare qualsiasi tipo di variabile ordinabile. Di seguito è riportata una versione ricorsiva dell’algoritmo in linguaggio C. L’algoritmo può restituire la posizione dell’elemento trovato all’interno dell’array A, oppure -1 se l’elemento non è stato trovato.
int binarySearch (int[] A, int primo, int ultimo, int val) {
int medio, ris = -1;
if (val < A[primo] || val > A[ultimo] )
return ris;
if (primo <= ultimo) {
medio = (primo + ultimo) / 2;
if (val < A[medio])
ris = binarySearch(A, primo, medio-1, val);
else if (val > A[medio])
ris = binarySearch(A, medio+1, ultimo, val);
else if (val == A[medio])
ris = medio;
}
return ris;
}
La complessità della singola chiamata alla funzione è $O(1)$ poichè non ci sono cicli e il numero di operazioni fatte non dipende da n. Bisogna quindi valutare quante volte la funzione viene chiamata. La funzione può richiamare sè stessa solamente una volta e ad ogni chiamata la distanza tra primo e ultimo si dimezza. Siccome il numero di chiamate affinchè la condizione “primo <= ultimo” diventi falsa è $log_2(n)$, Il numero di chiamate totali è $log_2(n)$. Per calcolare la complessità basta moltiplicare il numero di chiamate che è $O(log_2(n))$ per il peso di ogni chiamata che è $O(1)$ per ottenere la complessità:
\[T(n) = O(log_2(n))\]Esempio 6
Consideriamo il problema di calcolare l’ennesimo numero della successione di fibonacci e studiamo la complessità di un algoritmo ricorsivo che lo risolve. Il codice in linguaggio C è:
int fibonacci(int i) {
if (i < 0) return -1; // F(i) non e' definito per interi i negativi! */
if (i == 0) return 0;
else if (i == 1) return 1;
else return fibonacci(i-1) + fibonacci(i-2);
}
La singola chiamata della funzione ha complessità $O(1)$ poichè non ci sono cicli e il numero di operazioni fatte non dipende da n. La complessità è data quindi dal numero di chiamate della funzione. Siccome la funzione richiama sè stessa due volte, il numero di chiamate è 2n. La complessità totale dell’algoritmo è quindi
\[T(n) = O(2^n)\]Questo algoritmo è particolarmente poco efficiente poichè la funzione viene richiamata molte volte per gli stessi valori di i. Per risolvere tale problema è necessario trasformare la funzione nella sua versione iterativa oppure ricorrere ad una memoria che ci permette di salvare il valore calcolato dalla funzione per un certo valore di i e fare in modo che la funzione restituisca direttamente tale valore senza dover richiamare se stessa per i valori i-1 e i-2. Questo tipo di ragionamento è valido in generale per tutte quelle funzioni ricorsive che richiamano se stesse più di una volta comportando solitamente un numero di chiamate esponenziale.
Casi complessi
Ci sono algoritmi per cui il calcolo della complessità richiede lo studio di teoremi complessi come il “teorema principale” necessario per calcolare la complessità di molti algoritmi ricorsivi in particolare quelli con complessità pseudolineare, un esempio famoso è il merge sort. Vista l’eccessiva complessità di tali argomenti essi non verranno trattati.
La complessità dei problemi
Finora si è parlato della complessità degli algoritmi dando per scontato un concetto cioè che la complessità di un problema è dato dalla complessità del miglior algoritmo disponibile che lo risolve. Algoritmo e problema però sono due cose diverse e non è detto che al momento sia stato scoperto il milgior algoritmo possibile per un determinato problema. Ci si chiede quindi se sia possibila valutare la complessità intrinseca di un problema a prescindere dagli algoritmi al momento noti.
Complessità intrinseca di un problema
Un problema di cui si conosce un algoritmo, con la relativa complessità computazionale potrebbe, in futuro, essere risolto algoritmicamente in un altro modo, magari più efficiente (ad esempio con complessità di tempo inferiore)
- Fino a che punto è possibile “migliorare” la soluzione di un problema?
- Fino a che punto possiamo sperare che qualcuno in futuro possa formulare un algoritmo migliore per risolvere il nostro problema?
- Ci sono limiti al di sotto dei quali non è possibile scendere?
Per alcuni problemi la risposta è affermativa: si conosce il limite oltre il quale nessun algoritmo può scendere, per ingegnoso che possa essere.
Si parla di “lower bound” del problema, ovvero il numero minimo di operazioni che qualsiasi soluzione al problema comporta e che dipende dalla struttura stessa del problema mentre è indipendente da un qualsiasi algoritmo, anche sofisticatissimo. Il lower bound di un problema è una proprietà intrinseca dello stesso (spesso facciamo riferimento ad esso chiamandolo complessità intrinseca del problema), ed è un’informazione importantissima per chi sviluppa software.
La conoscenza del lower-bound di un problema ha un’importanza fondamentale: ci permette di non perdere tempo nella ricerca di un algoritmo più veloce, che non può esistere. Abbiamo così la certezza che nessun “genio” (neanche fra 10.000 anni) potrà mai trovare un algoritmo che sia più veloce del lower-bound del problema.
La dimostrazione di lower-bound è difficile. Bisogna analizzare, ad esempio, la natura del problema, indipendentemente da quella che può essere una possibile strategia di soluzione. Sono pochi i problemi di cui si è dimostrata l’esistenza di lower-bound. Due esempi famosi sono il problema della ricerca di un elemento in una tabella che è equivalente alla ricerca di una parola in un dizionario e il problema dell’ordinamento di una lista di oggetti (siano parole, numeri, ecc…). Nel primo caso il lower-bound è $log(n)$, cioè nessun algoritmo (basato su confronto di elementi) può impiegare, nel worst-case, meno di $log(n)$ operazioni in presenza di una tabella con n elementi. Nel secondo caso è stato dimostrato che un qualsiasi algoritmo che ordina un insieme di n elementi non può effettuare (nel worst-case) meno di $n·log(n)$ operazioni elementari.
Tipologia di problemi
I problemi possono essere di varia natura e in base al tipo quesito che pongono è possibile classificarli in quattro gruppi:
- problemi di decisione: un problema è di decisione se chiede di dare una risposta del tipo vero o falso, ad esempio dato un numero n determinare se esso è primo;
- problemi di ricerca: sono quei problemi che chiedono di trovare una soluzione corretta in un insieme di soluzioni possibili, ad esempio trovare un fattore primo di un numero può essere espresso come problema di ricerca che consiste nel trovare in un insieme di coppie (n, p) una coppia per cui p è un fattore primo di n;
- problemi di conteggio o enumerazione: sono quei problemi che chiedono di trovare il numero di soluzioni ad un dato problema di ricerca, ad esempio dato un numero n contare il numero di fattori primi di n;
- problema di ottimizzazione: sono quei problemi in cui si chiede di trovare la miglior soluzione possibile nell’insieme di tutte le soluzioni possibili di un problema di ricerca, ad esempio dato un grafo G trovare un insieme indipendente di G di dimensione massima.
- problema di funzione: sono quei problemi in cui ci si aspetta una singolo output per ogni input, ma l’output è più complesso di quello di un problema di decisione, cioè, non è solo sì o no;esempi notevoli includono il problema del commesso viaggiatore, che richiede la strada presa dal commesso viaggiatore, e il problema della fattorizzazione degli interi, che richiede la lista dei fattori.
Nonostante questi problemi siano apparentemente di natura molto diversa è in realtà possibile trasformare ogni problema in un problema di decisione riformulandolo opportunamente senza modificare il grado di complessità del problema. Le modalità in cui è possibile effettuare tale operazione sono complesse e richiederebbero uno studio più approfondito della teoria della computazione, basti sapere che è possibile farlo. Questo concetto è importante perchè ci permette di dire che nonostante i problemi si possano presentare sotto forme molto diverse, il modo in cui questo viene presentato non influisce sulla sua complessità poichè esso può essere riformulato in altri termini senza influire sulla sua complessità intrinseca. Sarà quindi ora possibile iniziare a catalogare i problemi in base alla loro complessità
Problemi computabili e non computabili
Preso un problema, di qualsiasi tipo esso sia, è possibile fare una prima catalogazione tra problemi risolvibili e problemi non risolvibli o comunque non sempre risolvibili. Preso l’insieme di tutti i possibili problemi immaginabili, il primo sottoinsieme è infatti l’insieme dei problemi computabili o decidibili. Tutti gli altri problemi saranno quindi chiamati non computabili o indecidibili
Un problema P si dice computabile quando esiste un algoritmo A che lo risolve, cioè applicando ad A una qualunque istanza I di P ne fornisce l’esatta soluzione in un numero finito di passi.
È importante sottolineare che l’algoritmo deve trovare la soluzione per ogni istanza del problema e che lo deve fare in un numero finito di passi, cioè in un tempo finito, impiegare un tempo infinito significherebbe infatti non trovare mai la soluzione.
La domanda che ci si pone è: i due sottoinsiemi appena identificati sono entrambi non vuoti? Sicuramente esistono problemi che sappiamo risolvere e problemi che non siamo in grado di risolvere, ma siamo proprio sicuri che i problemi che attualmente non siamo in grado di risolvere non possano avere una soluzione a noi sconosciuta? A questa domanda si è cercato di dare risposta per molto tempo e alla fine dell’800 con la teoria degli infiniti si era già riusciti a dare una risposta affermativa ma non era ancora stato formulato un problema per cui fosse anche stata dimostrata l’indecidibilità. Nel 1936 Alan Touring riuscì a dimostrare l’indecidibilità di un problema, il problema della terminazione (halting problem).
Problema della terminazione
Il problema della terminazione (dall’inglese Halting problem, tradotto anche con problema dell’arresto o problema della fermata) chiede se sia sempre possibile, descritto un algoritmo e un determinato ingresso finito, stabilire se l’algoritmo in questione termina o continua la sua esecuzione all’infinito. È stato dimostrato che non può esistere un algoritmo generale in grado di risolvere il problema per tutti i possibili ingressi. La versione più nota del problema è quella proposta nel 1936 dal matematico Alan Turing, insieme alla dimostrazione della sua indecidibilità.
Dimostrazione
Si supponga per assurdo che esista un algoritmo che prende in ingresso un qualsiasi altro algoritmo a avente un ingresso finito d ed è in grado di stabilire se a termina in tempo finito (restituendo il valore true) o se non termina (restituendo in questo caso il valore false).
// halts() restituisce true se il suo input termina, false altrimenti
boolean C(a, d):
return halts(a(d));
Essendo per la macchina sia a sia d sequenze indistinte di simboli, è possibile passare come secondo parametro di C lo stesso algoritmo a, ovvero eseguire C(a,a).
Sia ora loop un programma che non termina mai (ad esempio while true do done): è possibile costruire un altro algoritmo chiamato K che, prendendo in ingresso a, esegue loop non restituendo alcun valore se C(a,a) restituisce true, mentre restituisce true se C(a,a) restituisce false. Ovvero:
// loop() è una funzione che non termina
boolean K(a):
if C(a,a)
loop(); // non termina
else
return true; // termina
Quindi K termina restituendo il valore true solo se l’algoritmo a con ingresso a non termina, altrimenti K continua a eseguire loop ciclando all’infinito senza restituire alcun valore.
Passando all’algoritmo K lo stesso K, ovvero K(K), questo algoritmo termina, restituendo il valore true, solo se l’algoritmo K con input K non termina. Ovvero K(K) termina se e solo se K(K) non termina, il che è una contraddizione che prova essere assurda l’ipotesi iniziale sull’esistenza di un algoritmo C che, dato un qualsiasi algoritmo a e un suo input d, è in grado di stabilire se a(d) termina o non termina.
Problemi trattabili e intrattabili
Nell’analizzare la complessità degli algoritmi sono state identificate diverse classi di complessità e si è visto che ci sono classi di complessità per cui all’aumentare della dimensione dell’input il tempo di esecuzione rimane molto contenuto, per altri il tempo aumenta considerevolmente ma rimane ancora gestibile, ci sono altri casi, come ad esempio per la complessità esponenziale, in cui i tempi di calcolo diventano velocemente proibitivi. è evidente quindi che i problemi, possano essere catalogati tra problemi trattabili, quelli il cui tempo di calcolo non cresce in modo eccessivo, e quelli in cui i tempi di calcolo diventano proibitivi.
Di seguito sono riportati i tempi di esecuzione di algoritmi con diverse complessità di calcolo al variare della dimensione dell’input dando come tempo di esecuzione di un passo base 1 microsecondo (10-6 s)
| n = 10 | n=100 | n=1000 | n=106 | |
| log(n) | 10-6 | 2·10-6 | 3·10-6 | 6·10-6 |
| √n | 3·10-6 | 10-5 | 3·10-5 | 10-3 |
| n | 10-5 | 10-4 | 10-3 | 1 s |
| n·log(n) | 10-5 | 2·10-4 | 3·10-3 | 6 s |
| n2 | 10-4 | 10-2 | 1 s | 106 (~12 gg) |
| n3 | 10-3 | 1 s | 103 (~1 g) | 1012 (~30 secoli) |
| 2n | 10-3 | 1014 secoli | 10285 secoli | —- |
Guardando i risultati si può intuire che è possibile suddividere ulteriormente i problemi in problemi risolvibili velocimente e problemi trattabili ma trattabili solo quando n non cresce eccessivamente. Per un programmatore questa distinzione è importante poichè nella realtà passare da un tempo di calcolo quadratico ad uno pseudolineare rappresenta un salto di qualità decisamente notevole. Effettivamente i tempi polinomiali con esponente maggiore di 1 non sono particolarmente efficienti e ci si chiede se non sia opportuno ritenere anche i problemi con tale complessità intrattabili.
Per poter rispondere a questa domanda dobbiamo analizzare come cambiano i tempi di calcolo al variare della capacità computazionale dei calcolatori. Nella seguente tabella sono riportati i miglioramenti ottenibili, in termini di dimensioni delle istanze risolvibili, per diverse funzioni di complessità, al migliorare della tecnologia dei calcolatori. Con $x_i$ è indicata la dimensione di un’istanza risolvibile attualmente in un minuto per la i-esima funzione di complessità.
| T(n) | Computer odierno | Computer 100 volte più veloce | computer 10.000 volte più veloce |
|---|---|---|---|
| $n$ | $x_1$ | $100·x_1$ | $10.000·x_1$ |
| $n^2$ | $x_2$ | $10·x_3$ | $100·x_3$ |
| $n^3$ | $x_3$ | $4,6·x_3$ | $21,5·x_3$ |
| $n^5$ | $x_4$ | $2,5·x_4$ | $6,3·x_4$ |
| $2^n$ | $x_5$ | $x_5+6,6$ | $x_5+13,2$ |
| $3^n$ | $x_6$ | $x_6+4,2$ | $x_6+8,4$ |
Osservando i risultati riportati in tabella e considerando che, come indicato dalla legge di Moore, la potenza di calcolo dei calcolatori aumenta esponenzialmente raddoppiando ogni anno (anche se ci volesse più di un anno sarebbe comunque una crescita esponenziale), è lecito aspettarsi che un problema di complessità polinomiale oggi ritenuto intrattabile perchè presenta una dimensione dell’input troppo grande, diventerà trattabile in futuro con l’aumento delle capacità computazionali dei computer. Non si può dire la stessa cosa per i problemi esponenziali. Guardando il modo in cui sono stati ottenuti i risultati si può capire meglio quale sia l’entità dei miglioramenti ottenibili.
Considerando che:
\[\text{tempo di esecuzione} = \text{tempo esecuzione passo base} · \text{numero passi base}\] \[60s = tepb · T(n)\] \[T(n) = \frac{60s}{tepb}\]Se indichiamo con $n$ la dimensione dell’input per cui l’esecuzione dell’algoritmo richiede 1 minuto con un computer di riferimento, e con $n_x$ la dimensione dell’input per cui l’esecuzione dell’algoritmo richiede 1 minuto con un computer x volte più potente otteniamo che:
- algoritmo polinomiale di esponente k:
- algoritmo esponenziale di base k:
Bisogna poi ricordare che l’umento della potenza di calcolo x avviene in modo esponenziale. Per i problemi con complessità polinomiale significa quindi un miglioramento più che lineare nella dimensione dell’input infatti l’esponenziale domina la radice. Si può dire quindi che problemi di complessità polinomiale sono di per sè trattabili e il limite della dimensione dell’input che siamo in grado di gestire è puramente tecnologico.
Non si può fare la stessa osservazione per quanto riguarda i problemi esponenziali, per cui l’umento delle prestazioni esponenziale viene annullato dal logaritmo che è proprio la funzione inversa dell’esponenziale.
Se si ragionasse in termini di aumento del tempo di esecuzione dell’algoritmo invece che di aumento della potenza di calcolo si avrebbero gli stessi identici risultati, infatti dividere tepb per x (aumento delle prestazioni) o moltiplicare il tempo di calcolo (60s nell’esempio) per x (in questo caso aumento del tempo di calcolo) produce esattamente lo stesso risultato.
Possiamo quindi concludere che:
la distinzione tra problemi trattabili e intrattabili corrisponde alla distinzione tra problemi con complessità polinomiale e problemi con complessità esponenziale.
A scanso di errori (che gli studenti fanno molto spesso) è importante ricordare che i problemi intrattabili rientrano comunque nella categoria dei problemi computabili infatti i tempi di calcolo sono per noi inaccettabili ma finiti (e sempre risolvibili in tempi accettabili per valori di n molto piccoli).
Così come fatto in precedenza per i problemi indecidibili è necessario chiedersi se l’insieme dei problemi intrattabili o esponenziali è effettivamente un insieme non vuoto, infatti non basta non conoscere un algoritmo polinomiale che risolva un problema per sostenere che tale problema abbia complessità esponenziale, ma è necessaria una dimostrazione. Nel 1973 fu dimostrata per la prima volta la natura esponenziale di un problema, quello di stabilire se due espressioni regolari descrivono lo stesso insieme di stringhe.
Classi di complessità P e NP
L’insieme dei problemi che sono risolvibili in tempo polinomiale è chiamato P che stà appunto per “polinomiale”. Sono esempi di problemi P tutte le operazioni aritmetiche, decidere se un numero è primo…
Esiste poi una particolare classe di problemi che non sono risolvibili in tempo polinomiale ma per cui, è possibile verificare in tempo polinomiale se una specifica soluzione del problema sia corretta oppure no chiamata NP. Un esempio di questo tipo di problemi è il gioco del sudoku per cui non è possibile trovare la soluzione corretta in tempo polinomiale ma è un problema P verificare che una certa soluzione sia corretta. Sebbene questo esempio sia abbastanza intuitivo non è facile da formalizzare e dimostrare. Un secondo famosissimo esempio è il problema di trovare in un grafo un ciclo hamiltoniano cioè un cammino chiuso che includa tutti i nodi del grafo una sola volta (il primo e l’ultimo nodo per chiudere il cammino sono lo stesso nodo che può quindi ripetersi). Il problema è detto anche “problema del commesso viaggiatore” che deve raggiungere tutti i luoghi su una mappa evitando di passare più volte nello stesso posto.
Il nome NP deriva da “non-deterministico polinomiale” e per capire questa definizione è necessario spiegare il significato di determinismo. Un algoritmo è deterministico quando dato un certo stato dell’esecuzione, l’azione successiva può essere soltanto una, determinata dallo stato attuale. Si dice invece non deterministico un algoritmo che in un certo stato di esecuzione può svolgere azioni differenti, tale scelta può avvenire secondo i criteri più disparati (se casuale si parla di algoritmi probabilistici e formano una classe di algoritmi ancora differente). Normalmente quindi un algoritmo non deterministico può dare risultati differenti a partire da uno stesso input.
Nel caso dei problemi NP il concetto di non determinismo in realtà è diverso e un po’ particolare. Prendendo ad esempio il problema del ciclo hamiltoniano possiamo immaginare un algoritmo che ogni volta che deve scegliere il prossimo nodo del grafo da visitare (nella realtà scegliere la strada ad un bivio) è in grado di esplorare contemporaneamente tutti i percorsi possibili. In pratica in questo contesto un algoritmo non deterministico è inteso come un algoritmo eseguito con infinita capacità di parallelismo. Se un algoritmo con tali caratteristiche è in grado di risolvere un problema in tempo polinomiale allora tale problema è un problema NP.
Poiché un algoritmo deterministico può essere visto come caso particolare di un algoritmo non-deterministico − o anche, più semplicemente, poiché un problema risolvibile in tempo polinomiale è evidentemente verificabile in tempo polinomiale − la classe P è inclusa nella classe NP. Sul viceversa ci sono forti dubbi, sebbene nessuno sia ancora riuscito a dimostrare che P sia inclusa strettamente in NP, ossia che per almeno uno dei problemi in NP non esistano algoritmi risolutivi tempo-polinomiali. In effetti, si tratta di una delle più importanti questioni aperte nella teoria della complessità computazionale. In rete cercando “P vs NP” è possibile trovare molte informazioni a riguardo tra cui un interessante video (che puoi trovare qui) che ti consiglio di guardare che spiega in maniera chiara ed intuitiva la natura del problema oltre che descrivere le classi P ed NP.
Per approfondire la natura del problema è necessario studiare un sottoinsieme particolare di NP, la classe dei problemi NP-completi.
Classe dei problemi NPC o NP-Completi
Dagli anni ’70 del secolo scorso, sono stati individuati parecchi tra i problemi “più difficili” della classe NP, detti NP-completi: ciò significa che qualunque problema in NP può essere “trasformato”, in tempo polinomiale, in uno di essi. In particolare, i dati in ingresso per il primo problema sono presi da un algoritmo tempo-polinomiale, che produce i dati in ingresso per il secondo problema, in modo tale che la risposta del secondo problema sia esattamente quella che darebbe il primo. Dunque, tutti i problemi appartenenti alla sottoclasse degli NP-completi presentano lo stesso livello di difficoltà (intesa come laboriosità richiesta per risolverli) e ognuno di essi può essere trasformato efficientemente in ciascun altro appartenente alla stessa sottoclasse.
Tutto ciò implica che, qualora si trovasse un algoritmo tempo-polinomiale per risolvere uno qualsiasi dei problemi NP-completi, ecco che si sarebbe trovata una soluzione efficiente per tutti i problemi in NP, e quindi l’intera classe NP “collasserebbe” nella classe P.
Per concludere che le due classi sono diverse, sarebbe invece sufficiente provare la non esistenza di un algoritmo tempo-polinomiale per uno qualsiasi dei problemi in NP. In un fondamentale articolo del 1971, Stephen A. Cook dimostrò che qualsiasi problema in NP può essere trasformato nel problema della soddisfacibilità, e quindi fu questo il primo problema NP-completo ad essere individuato.
Il problema della soddisfacibilità (SAT) è così definito: data una proposizione formata dalla congiunzione (o and locico, ∧) di clausole, ciascuna costituita da una disgiunzione (or logico, ∨) di letterali (cioè di variabili booleane o di loro negazioni), stabilire se esiste una assegnazione di valori di verità alle variabili che vi occorrono, tale che la proposizione risulti vera (esempio di proposizione formata da tre clausole: $(\lnot x_1 ∨ x_2 ∨ \lnot x_3) ∧ (x_1) ∧ (\lnot x_2 ∨ x_3)$).
Qui non ci addentreremo nell’analisi del problema che puoi approfondire qui
Negli anni seguenti furono trovati moltissimi problemi che possono essere trasformati in tempo polinomiale in SAT (o viceversa) andando ad ingrandire l’insieme dei problemi NPC.
Altre considerazioni su P e NP
Nonostante la classe NP indichi nella sua definizione il fatto che essi possano essere risolti in tempo polinomiale è importante sottolineare che questo può avvenire solo se si ha a disposizione un grado di parallelismo infinito, ma questo nella realtà non è possibile. Con i computer reali che usiamo tutti i giorni è possibile eseguire solamente algoritmi deterministici e sebbene a volte si possa riuscire ad ottenere un certo grado di parallelismo questo è molto limitato e di certo non infinito. Per questo motivo con i computer reali i problemi considerati appartenenti ad NP e non a P sono attualmente risolvibili solo in tempi esponenziali e questo rimarrà vero a meno che non si trovi un algoritmo con complessità polinomiale per un problema NP di fatto spostando il problema in P. Se questo problema fosse un problema NPC, l’intera classe NP collasserebbe in P.
Classe NP-difficile o NP-Hard

Diagramma di Eulero-Venn per le classi di complessità P, NP, NP-Completo e NP-hard.

Diagramma di Eulero-Venn per le classi di complessità P, NP, NP-Completo e NP-hard.
In teoria della complessità, i problemi NP-difficili o NP-ardui (in inglese NP-hard, da nondetermistic polynomial-time hard problem, “problema difficile non deterministico in tempo polinomiale”) sono una classe di problemi che può essere definita informalmente come la classe dei problemi almeno difficili come i più difficili problemi delle classi di complessità P e NP. Più formalmente, un problema H è NP-difficile se e solo se ogni problema NP L è polinomialmente riducibile ad H. Da questa definizione si ricava che i problemi NP-difficili sono non meno difficili dei problemi NP-completi, che a loro volta sono per definizione i più difficili delle classi P/NP.
La classe dei problemi NP-difficili ha una grande rilevanza sia teorica che pratica. In pratica, dimostrare che un problema di calcolo è equivalente a un problema notoriamente NP-difficile significa dimostrare che è praticamente impossibile trovare un modo efficiente di risolverlo, cosa che ha molte implicazioni in informatica. Da un punto di vista teorico, lo studio dei problemi NP-difficili è un elemento essenziale della ricerca su alcuni dei principali problemi aperti della complessità.
Classe EXP o a tempo-esponenziale
La classe di complessità più vicina alle classi P e NP è la classe dei probemi con complessità esponenziale. I problemi per cui è possibile almeno verificare se una soluzione sia corretta in tempo polinomiale ricadono nell’insieme NP, esistono però problemi per cui nemmeno questo è possibile, ad esempio nel gioco degli scacchi non solo è difficile dire quale sia la mossa migliore da fare, ma non è nemmeno possibile verificare se una mossa o una serie di mosse siano quelle migliori. Problemi come questo fanno parte della classe dei problemi EXP o a tempo-esponenziale.
Algoritmi probabilistici
Esistono moltisimi problemi di cui non si conosce una soluzione polinomiale ma per cui è necessario trovare la soluzione in moltissime applicazioni come quelle legate alla crittografia, basti pensare che fino a pochi anni fa non era nota una soluzione polinomiale per verificare la primalità di un numero. Per questo motivo è necessario trovare dei sistemi che ci permettano di trovare in tempi accettabili delle soluzioni accettabili. Che cosa intendiamo però per accettabili? è possibile ad esempio trovare soluzioni approssimate o soluzioni che siano esatte ma solo con un certo grado di sicurezza. Algoritmi che siano in grado di fornire tali soluzioni sono gli algoritmi probabilistici.
Gli algoritmi probabilistici sono quegli algoritmi che quando devono prendere una decisione possono farlo in modo casuale, salla base di un estrazione di un valore casuale. L’estrazione di un numero casuale in informatica è però un problema piuttosto delicato, infatti i generatori di numeri casuali reali sono molto costosi e difficili da reperire poichè sono basati su sistemi quantistici particolari, nella quasi totalità dei casi quindi gli algoritmi probabilistici si basano sulla generazione di sequenze di numeri pseudo-casuali e la costruzione di questi generatori e la loro non prevedibilità da parte di terzi è alla base della sicurezza di molti sistemi crittografici.
Un generatore di numeri pseudo-casuali è una funzione deterministica in grado di generare una sequenza di valori x1, . . . , xn indistinguibile da un’altra sequenza di valori casuali y1, . . . , yn in tempo polinomiale.
Esistono essenzialmente tre tipi di algoritmi probabilistici:
- Algoritmi numerici: per fornire un risultato approssimato con una certa confidenza.
Esempio: Con probabilità 90% la risposta è 60 ± 1. Più volte si esegue l’algoritmo, maggiore diventa la precisione o la confidenza. - Algoritmi di Monte Carlo: per fornire un risultato esatto con alta probabilità benché talvolta possano fornire una risposta errata.
Esempio: Con probabilità 99%, la risposta è 60. Più si esegue l’algoritmo, maggiore diventa la probabilità che il risultato sia esatto (vedi classe BPP). - Algoritmi Las Vegas per fornire un risultato esatto con certezza ma in un tempo probabilistico, in pratica ho una certa probabilità che la risposta venga data in un certo tempo. L’algoritmo può anche non rispondere poichè per stare nei tempi stabiliti l’esecuzione viene fermata (vedi classe ZPP)
. Esempio: La risposta è 60.
Per capire meglio il comportamento di questi algoritmi assumiamo che si voglia costruire un algoritmo probabilistico che stampi le date di eventi storici. Alla domanda “Quando Cristoforo Colombo scoprì l’America?”, le risposte che si possono ottenere dai tre tipi di algoritmi, eseguiti per 5 volte consecutive, sono del tipo:
- Algoritmo numerico: 1490 ± 10, 1485 ± 10, 1492 ± 10, 1491 ± 10, 1492 ± 10;
- Algoritmo di Monte Carlo: 1492, 1500, 1492, 1492, 1491;
- Algoritmo Las Vegas: 1492, no ouput, 1492, 1492, no output.
Questi metodi ci permettono quindi di ottenere soluzioni più o meno approssimate o sicure a problemi per cui ottenere una soluzione esatta richiederebbe un tempo non polinomiale. Il grado di approssimazione o di sicurezza della soluzione può essere deciso a priori aumentando o diminuendo il tempo di calcolo.
Gli argoritmi probabilistici ci consentono di identificare nuove classi di problemi risolti con questo genere di algoritmi.
Classe BPP
La classe dei problemi BPP (Bounded-error Probabilistic Polynomial time, “tempo polinomiale probabilistico con errore limitato”) contiene quei problemi che richiedono un tempo polinomiale per avere una soluzione probabilistica corretta. Più precisamente, essi sono risolvibili in tempo polinomiale da un algoritmo probabilistico (la definizione reale dice “da una macchina di Turing probabilistica” ma si dovrebbe approfondire l’argomento che è lungo), con una probabilità di errore al massimo di 1/3 per tutte le istanze.
| Algoritmo BPP (1 esecuzione) | ||
|---|---|---|
| Risposta prodotta | ||
| Risposta corretta | SÌ | NO |
| SÌ | ≥ 2/3 | ≤ 1/3 |
| NO | ≤ 1/3 | ≥ 2/3 |
| Algoritmo BPP (k esecuzioni) | ||
| Risposta prodotta | ||
| Risposta corretta | SÌ | NO |
| SÌ | > 1 − 2−ck | < 2−ck |
| NO | < 2−ck | > 1 − 2−ck |
| per una qualche costante c > 0 | ||
In pratica, una probabilità di errore di 1/3 potrebbe non essere accettabile, tuttavia, la scelta di 1/3 nella definizione è arbitraria. Può essere qualsiasi costante c fra 0 e 1/2 (esclusiva). Il limite di 1/2 è importante perchè ci permette di eseguire l’algoritmo molte volte, riducendo progressivamente la probabilità di errore. Per creare un algoritmo estremamente accurato basterà semplicemente eseguire l’algoritmo molte volte. In pratica si può decidere a piacere il grado di sicurezza della soluzione aumentando o diminuendo il tempo di calcolo.
Un analisi dettagliata (ma che trascuriamo per la sua complessità) mostra che variando il numero di esecuzioni è possibile ottenere un errore elevato fino a $1/2 − n^{−c}$ da un lato, o un errore piccolo fino a $2^{−n^c}$ dall’altro, dove c è una qualsiasi costante positiva, ed n è la lunghezza dell’input.
La definizione della classe BPP è quasi identica a quella della classe PP che è la classe di problemi risolvibili in tempo polinomiale da un una macchina di Turing probabilistica con una probabilità di meno di 1/2 per tutte le istanze. In pratica PP è la generica classe dei problemi risolti con algoritmi probabilistici (algoritmi Monte Carlo). La differenza è sottile e non ci addentreremo in questa questione, diremo solo che questo ci permette di avere algoritmi efficienti poichè il vincolo (il valore c) ci permette di ridurre abbastanza velocemente l’errore all’aumentare del numero di esecuzioni.
Relazione con altre classi di complessità
BPP è una delle più grandi classi “pratiche” di problemi, vale a dire che la maggior parte dei problemi di interesse in BPP hanno algoritmi probabilistici efficienti che possono essere eseguiti su macchine moderne reali. Per questa ragione è di grande interesse pratico quali problemi e classi di problemi siano all’interno di BPP. BPP contiene anche P, la classe dei problemi risolvibili in tempo polinomiale con una macchina deterministica, dal momento che una macchina deterministica è un caso speciale di una macchina probabilistica.
Oltre ai problemi in P, che sono ovviamente in BPP, si conoscevano molti problemi che erano in BPP ma non in P. Il numero di tali problemi sta diminuendo, e si congettura che P = BPP.
Per molto tempo, uno dei problemi più famosi che si conosceva essere in BPP ma non essere in P era il problema di determinare se un numero dato è primo. Tuttavia, nel 2002 è stato trovato un algoritmo deterministico in tempo polinomiale per questo problema, dimostrando così che è in P.
Un esempio importante di un problema in BPP che ancora non si conosce in P è la verifica dell’identità dei polinomi, il problema di determinare se un polinomio è identicamente uguale al polinomio zero. In altre parole, c’è un’assegnazione di variabili tale che quando si calcola il polinomio il risultato è diverso da zero? È sufficiente scegliere il valore di ciascuna variabile uniformemente a caso da un sottoinsieme finito di almeno d valori per ottenere una probabilità di errore vincolato, dove d è il grado totale del polinomio. Questo problema è un problema NP.
Possiamo quindi dire che $P \subseteq ZPP \subseteq BPP \subseteq PP$ ma non sappiamo che relazione abbia BPP con NP
Nella definizione della classe, se sostituiamo la macchina di Turing (io ho fin qui semplificato parlando genericamente di algoritmo deterministico) comune con un computer quantistico, otteniamo la classe BQP.
Classe BQP

La presunta relazione di BQP con gli spazi di altri problemi.

La presunta relazione di BQP con gli spazi di altri problemi.
Nella teoria della complessità computazionale, BQP (Bounded-error Quantum Polynomial-time, “tempo polinomiale quantistico con errore limitato”) è una classe di complessità a cui appartengono quei problemi che richiedono un tempo polinomiale da parte di un computer quantistico per avere una soluzione corretta con probabilità maggiore o uguale a 2/3 e quindi, corrispondentemente, con una probabilità di errore minore o uguale a 1/3. È l’analogo quantistico della classe BPP.
In altre parole, c’è un algoritmo per un computer quantistico (un algoritmo quantistico) che risolve il problema decisionale con un’alta probabilità ed è garantito che si esegue in tempo polinomiale. In qualsiasi esecuzione data dell’algoritmo, ha una probabilità al massimo di 1/3 di dare la risposta sbagliata. Analogamente ai gli algoritmi BPP è possibile aumentare il numero di esecuzioni per ridurre a piacere l’errore fino a $2^{−n^c}$.
Computazione quantistica
Il numero di qubit nel computer può essere una funzione polinomiale della dimensione dell’istanza. Ad esempio, è noto che alcuni algoritmi fattorizzano un intero di n bit usando poco più di 2n qubit (algoritmo di Shor).
Solitamente, la computazione su un computer quantistico finisce con una misurazione. Questo conduce a un collasso dello stato quantistico a uno degli stati fondamentali. Si può dire che si misura che lo stato quantico è nello stato corretto con un’alta probabilità.
I computer quantistici hanno ottenuto interesse diffuso perché è noto che alcuni problemi di interesse pratico sono in BQP, ma si sospetta che siano fuori da P. Alcuni esempi rilevanti sono:
- Fattorizzazione degli interi (vedi l’algoritmo di Shor)
- Logaritmo discreto
- Simulazione di sistemi quantistici (vedi simulatore universale quantico)
- Calcolo del polinomio di Jones in certe radici unitarie
Relazione con altre classi di complessità
BQP contiene P e BPP ma non è nota la sua relazione con NP anche perchè questo significherebbere conoscere anche la relazione tra P e NP.
Esiste una classe chiamata QMA che è in relazione a BQP così come NP lo è con P, in pratica è quella classe di problemi per cui data una soluzione è possibile valutarla in tempo polinomiale con un computer quantistico. Come per P vs NP non è noto se i due insiemi sono uguali o no.
$P \subseteq BPP \subseteq BQP \subseteq QMA \subseteq PP \subseteq PSPACE \subseteq EXP$
Classe ZPP
Nella teoria della complessità computazionale, ZPP (Zero-error Probabilistic Polynomial time, “tempo polinomiale probabilistico con errore zero”) è la classe di complessità dei problemi per i quali esiste una macchina di Turing probabilistica (algoritmo probabilistico) con queste proprietà:
- Restituisce sempre la risposta corretta SÌ o NO.
- Il tempo di esecuzione è polinomiale in termini di aspettativa per ogni input.
In altre parole, se l’algoritmo può lanciare una moneta veramente casuale mentre è in esecuzione, restituirà sempre la risposta corretta e, per un problema di dimensione n, c’è un qualche polinomio p(n) tale che il tempo medio di esecuzione sarà minore di p(n), anche se potrebbe essere occasionalmente molto più lungo. Tale algoritmo è chiamato algoritmo Las Vegas.
Altre classi di complessità
Le classi di complessità in cui sono stati suddivisi i problemi sono moltissime e non riguardano solo la complessità di tempo. Qui puoi trovarne un elenco.
Siccome le classi sono moltissime e non sono note le relazioni tra molte di esse, fornire un diagramma esaustivo che rappresenti correttamente e contemporaneamente tutte le classi di complessità è impossibile. Di seguito sono riportati alcuni diagrammi.


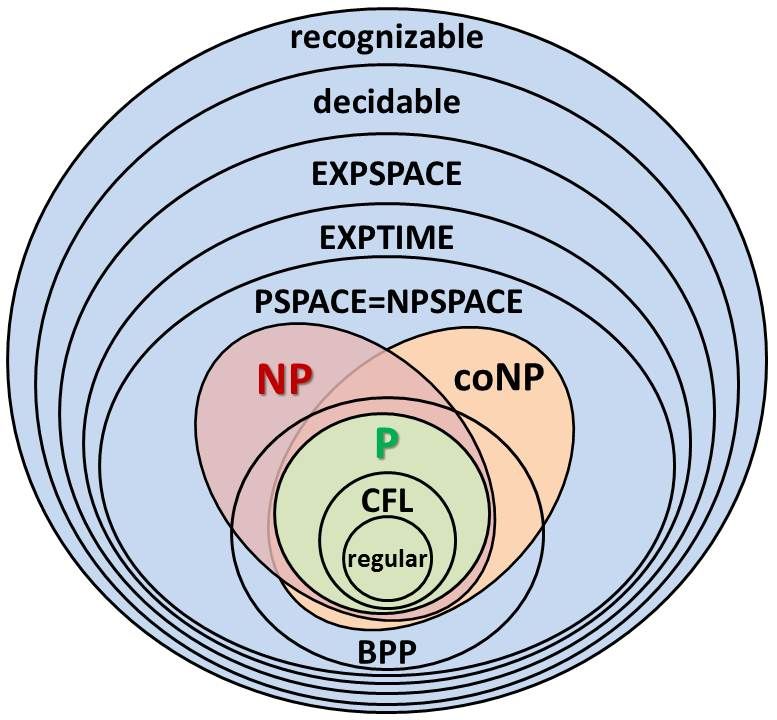

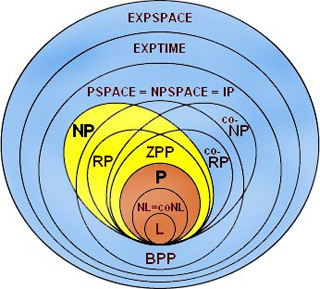

Riferimenti esterni
- Teoria della complessità computazionale su Wikipedia
- Notazione O-grande su Wikipedia
- Algoritmi di ordinamento su Wikipedia
- Complessità intrinseca di un problema: dispensa del Prof. Alberto Postiglione per il corso “Concetti di Base su Algoritmi, Strutture Dati e Programmazione” dell’Università degli Studi di Salerno.
- Problema computazionale su Wikipedia
- Problema della terminazione su Wikipedia
- Legge di Moore su Wikipedia
- Lorenzo Repetto - Dai giochi agli algoritmi, un’introduzione non convenzionale all’informatica - Edizioni Kangarou Italia 2019 - ISBN 978-88-89249-62-8
- “P vs. NP and the Computational Complexity Zoo” su Youtube
- NP-difficile su Wikipedia
- Dispense per il corso “Insegnamento di algoritmi avanzati” di Roberto Posenato
- Dispense per il corso “Algoritmi e strutture dati” di Alberto Montresor, Università di Trento
- BPP su Wikipedia
- PP su Wikipedia
- BQP su Wikipedia
- ZPP su Wikipedia
- Glossario delle classi di complessità su Wikipedia